Planar biaxial tests $($Fig $1($a$))$ are typically used to extract the mechanical properties of a wide range of materials, including metals, polymers, and biological tissues, especially if the properties are anisotropic. For biological tissue samples, the specimen is stretched with hooks that are connected to linear actuators. During the test, biaxial forces are measured from load cells, displacement can be measured by optically tracking markers that are placed on the surface of the specimen. This force$-$displacement data can then be converted to stress$-$strain curves, which reveal the underlying mechanical behavior of the tissue specimen.

Computational models, such as finite element analysis $($FEA$),$ can be used to simulate and compute key mechanical variables during planar biaxial tests. Fig $1($b$)$ shows a FEA model of biaxial test. From the FEA simulation, the stress$-$strain of the two directions $(11$ and $22)$ can be obtained $($Fig $1($c$)).$

In this project, you will work with the stress$-$strain data and complete a series of tasks outlined below. In the real world, these tasks are useful for finding the stiffness of material at various loading conditions, the strain energy density of the material, stress distribution in the deformable body, etc.

To begin with, the stress$-$strain data can be found in Data.mat. Use the PYTHON code below to import the data.

import scipy

DataRead$=$scipy.io$.$loadmat$(\text{'}$C:$/.../$Data$.$mat'$)$ # replace with the directory containing 'Data.mat' Data$=$DataRead$[\text{'}$Data$\text{'}]$

Or

from scipy import io

DataRead$=$io$.$loadmat$(\text{'}$C:$/.../$Data$.$mat'$)$ # replace with the directory containing 'Data.mat'

Data$=$DataRead$[\text{'}$Data$\text{'}]$

In the $2$D array 'Data', rows correspond to data points, $1^{st}$ to $5^{th}$ columns correspond to time, strain E$11,$ strain E$22,$ stress S$1,$ and stress S$22,$ respectively. $11$ and $22$ stand for two directions in the biaxial test. For the following questions, use built$-$in functions whenever possible.

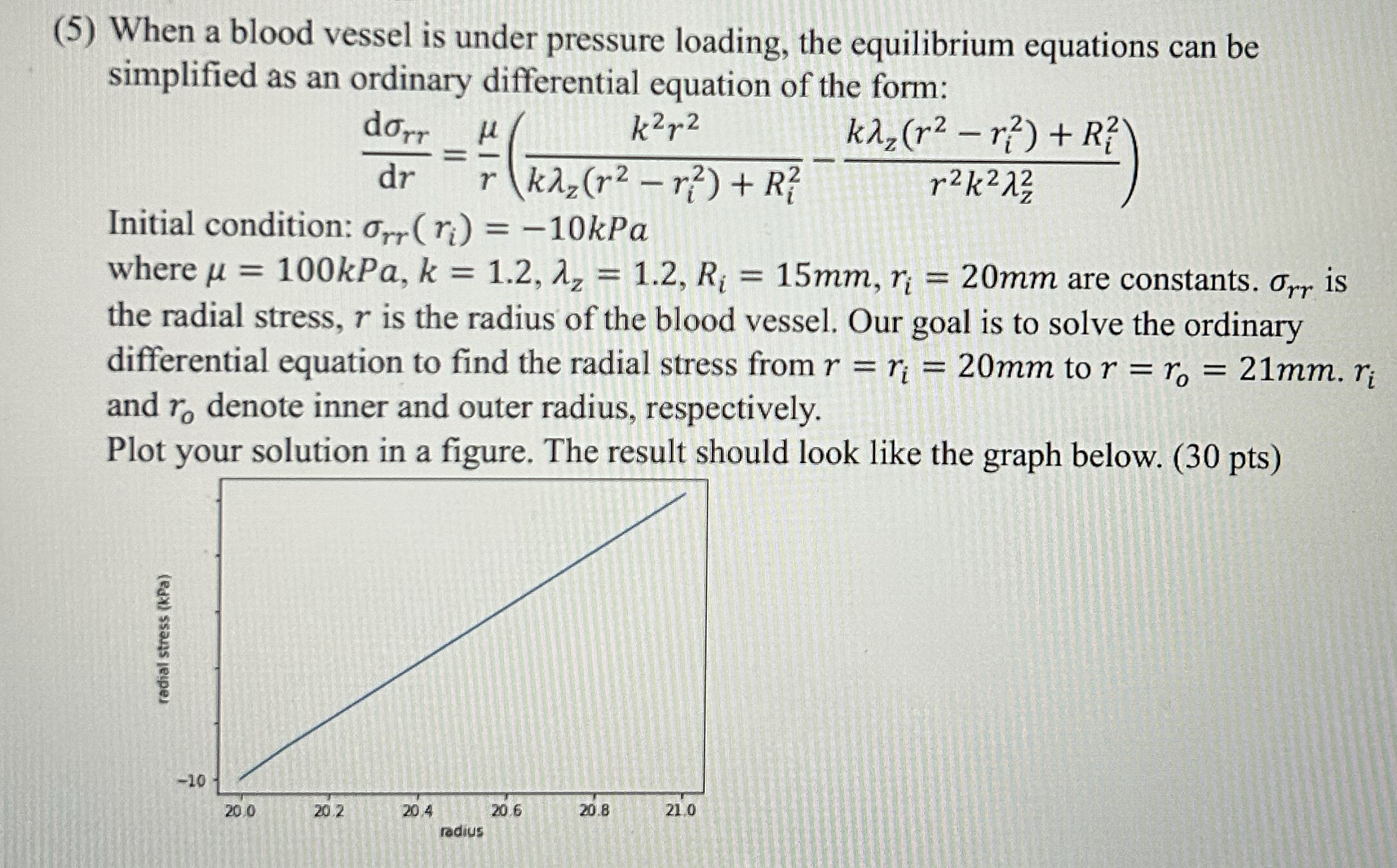
$(5)$ When a blood vessel is under pressure loading, the equilibrium equations can be simplified as an ordinary differential equation of the form:

$\frac{d{}_{rr}}{(d)r}=\frac{}{r}(\frac{k^2{r}^2}{k{}_z(r^2-r_i^2)+R_i^2}-\frac{k{}_z(r^2-r_i^2)+R_i^2}{r^2{k}^2{}_z^2})$

Initial condition: ${}_{rr}(r_i)=-10$kPa

where $=100$kPa,$k=1\mathrm{.}2,{}_z=1\mathrm{.}2,R_i=15mm,r_i=20mm$ are constants. ${}_{rr}$ is the radial stress, $r$ is the radius of the blood vessel. Our goal is to solve the ordinary differential equation to find the radial stress from $r=r_i=20mm$ to $r=r_o=21mm.r_i$ and $r_o$ denote inner and outer radius, respectively.

Plot your solution in a figure. The result should look like the graph below. $(30$ pts $)$