Question: Plane strain problems: In many situations, physical constraints prevent strain from occurring in a given direction. For example, epsi _ ( z ) =
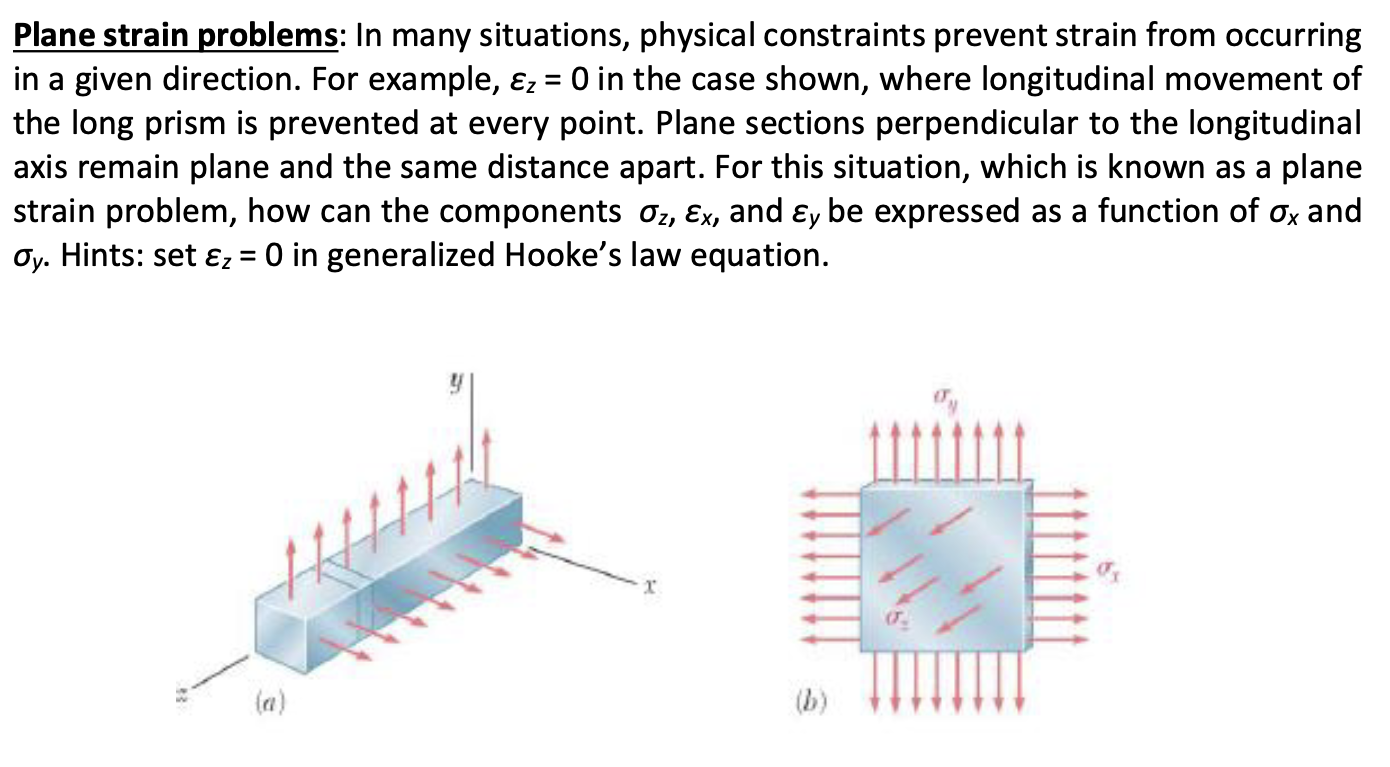
Plane strain problems: In many situations, physical constraints prevent strain from occurring
in a given direction. For example, epsi z in the case shown, where longitudinal movement of
the long prism is prevented at every point. Plane sections perpendicular to the longitudinal
axis remain plane and the same distance apart. For this situation, which is known as a plane
strain problem, how can the components sigma zepsi x and epsi y be expressed as a function of sigma x and
sigma y Hints: set epsi z in generalized Hooke's law equation.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


