Please answer all questions clearly.

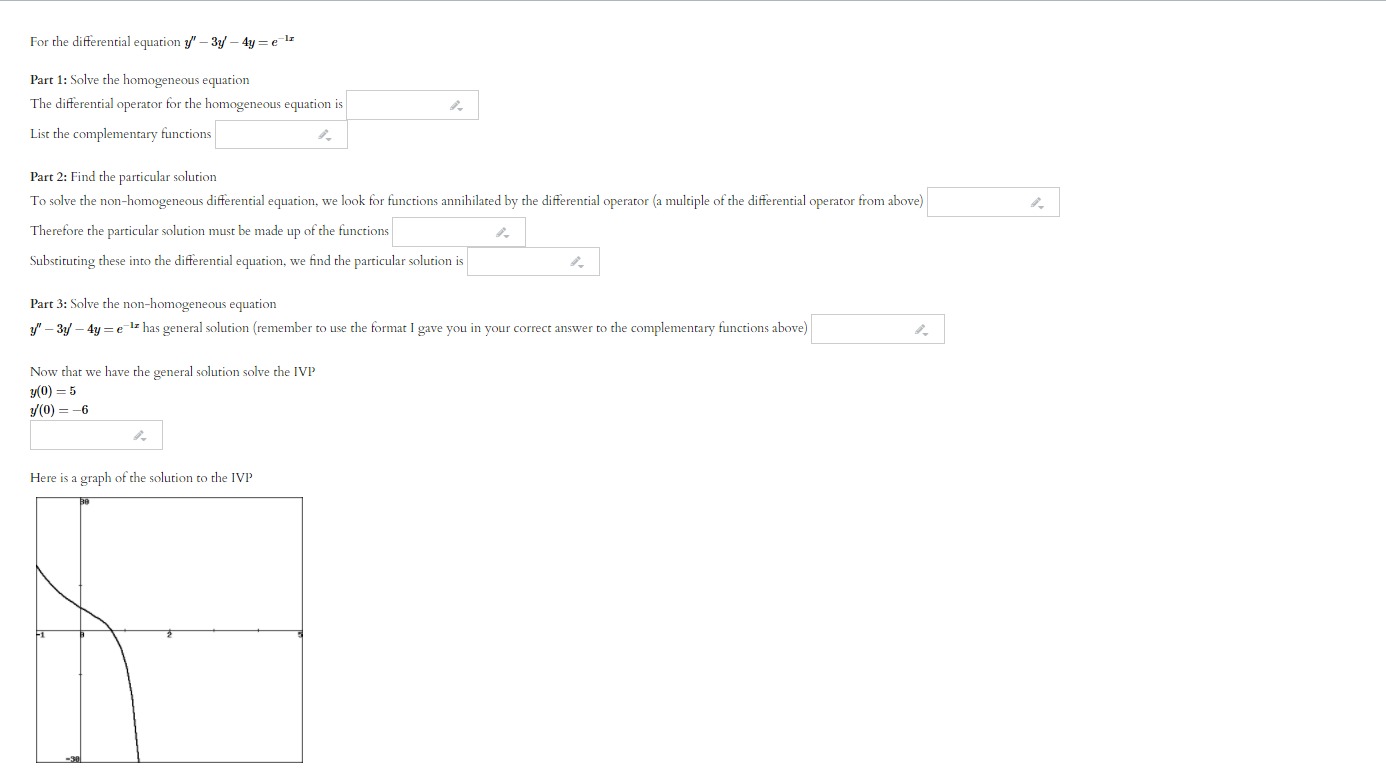
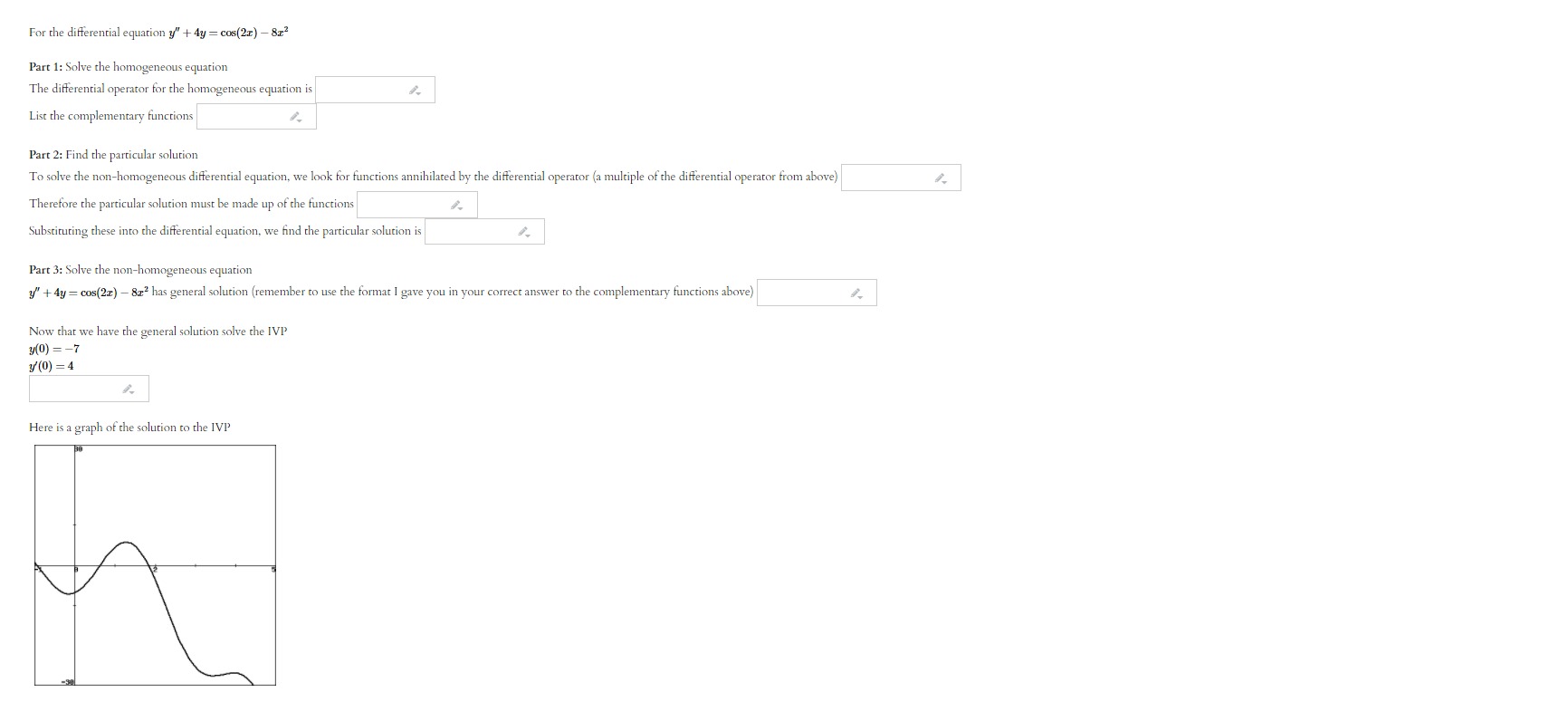
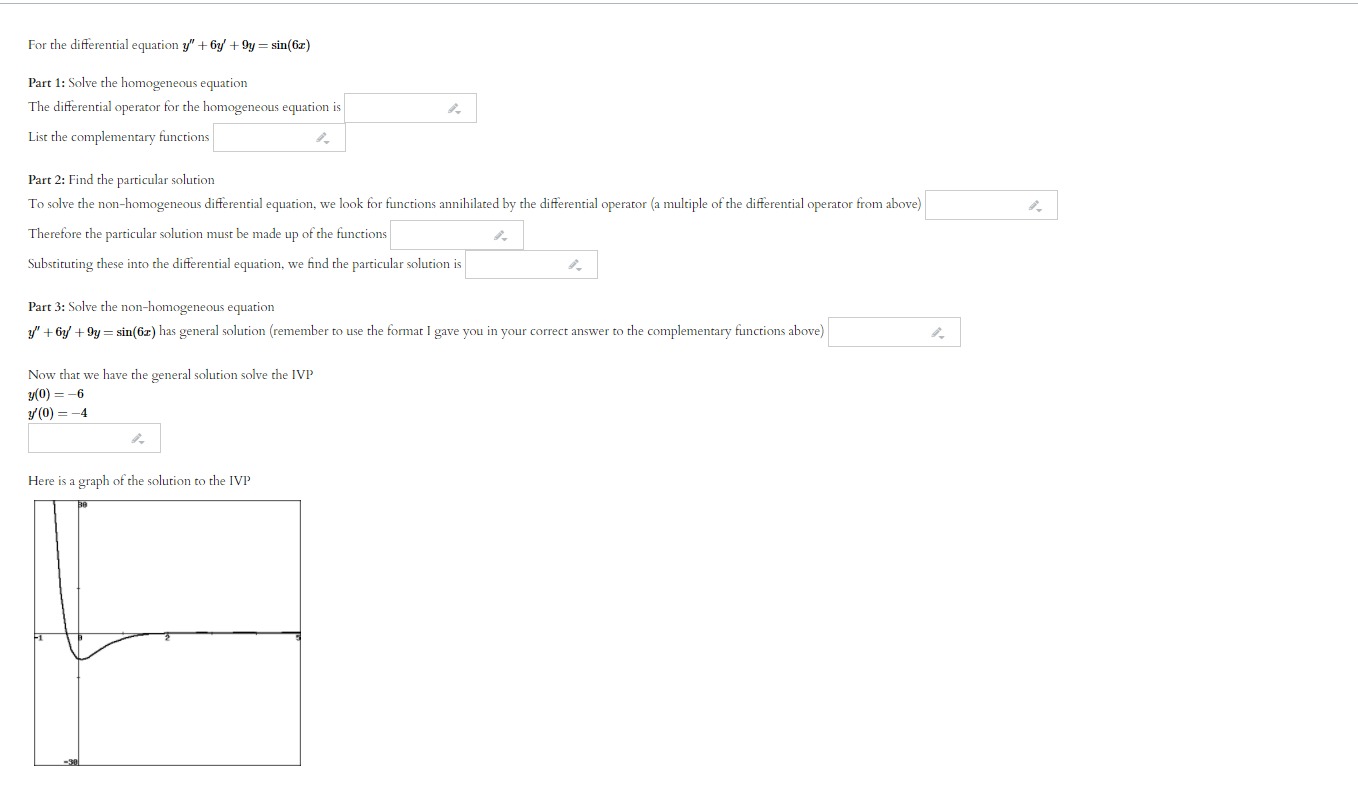
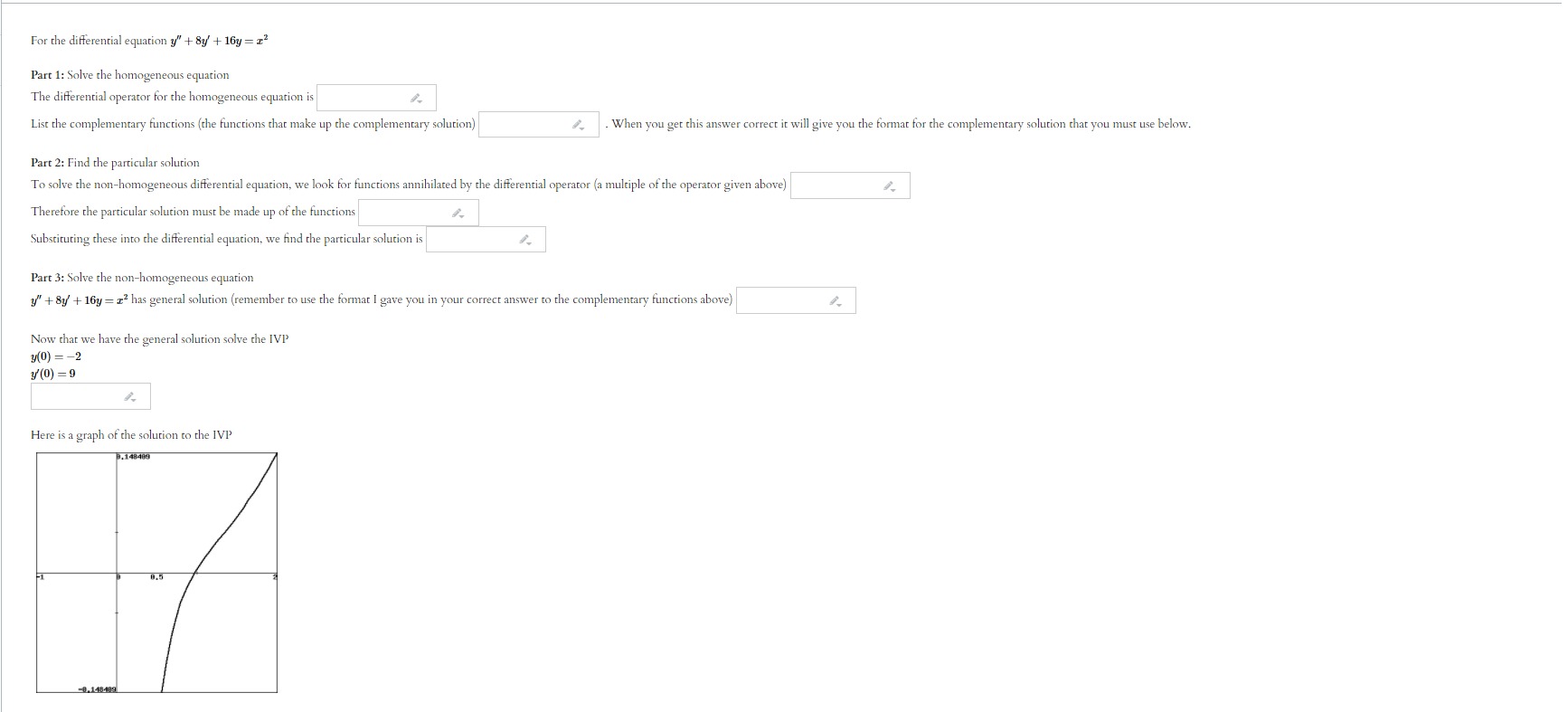
For the differential equation ?" - 3y' - Ay = e-1x Part 1: Solve the homogeneous equation The differential operator for the homogeneous equation is List the complementary functions Part 2: Find the particular solution To solve the non-homogeneous differential equation, we look for functions annihilated by the differential operator (a multiple of the differential operator from above Therefore the particular solution must be made up of the functions Substituting these into the differential equation, we find the particular solution is Part 3: Solve the non-homogeneous equation y" - 3y - 4y = e Iz has general solution (remember to use the format I gave you in your correct answer to the complementary functions above) Now that we have the general solution solve the IVP y(0) =5 y'(0) = -6 Here is a graph of the solution to the IVPFor the differential equation y" + 4y = cos(2x) - 8x2 Part 1: Solve the homogeneous equation The differential operator for the homogeneous equation is List the complementary functions Part 2: Find the particular solution To solve the non-homogeneous differential equation, we look for functions annihilated by the differential operator (a multiple of the differential operator from above) Therefore the particular solution must be made up of the functions Substituting these into the differential equation, we find the particular solution is Part 3: Solve the non-homogeneous equation y" + 4y= cos(21) - 812 has general solution (remember to use the format I gave you in your correct answer to the complementary functions above) Now that we have the general solution solve the IVP y(0) = -7 y'(0) = 4 Here is a graph of the solution to the IVPFor the differential equation y" + 6y' + 9y = sin(61) Part 1: Solve the homogeneous equation The differential operator for the homogeneous equation is List the complementary functions Part 2: Find the particular solution To solve the non-homogeneous differential equation, we look for functions annihilated by the differential operator (a multiple of the differential operator from above) Therefore the particular solution must be made up of the functions Substituting these into the differential equation, we find the particular solution is Part 3: Solve the non-homogeneous equation y" + 6y + 9y= sin(61) has general solution (remember to use the format I gave you in your correct answer to the complementary functions above) Now that we have the general solution solve the IVP y(0) = -6 y'(0) = -4 Here is a graph of the solution to the IVPFor the differential equation y" + 8y' + 16y = 12 Part 1: Solve the homogeneous equation The differential operator for the homogeneous equation is List the complementary functions (the functions that make up the complementary solution) . When you get this answer correct it will give you the format for the complementary solution that you must use below. Part 2: Find the particular solution To solve the non-homogeneous differential equation, we look for functions annihilated by the differential operator (a multiple of the operator given above) Therefore the particular solution must be made up of the functions Substituting these into the differential equation, we find the particular solution is Part 3: Solve the non-homogeneous equation y" + 8y + 16y = 12 has general solution (remember to use the format I gave you in your correct answer to the complementary functions above) Now that we have the general solution solve the IVP y(0) =-2 y'(0) =9 Here is a graph of the solution to the IVP P.148409 50.148409