Please answer both of these problems if you can. I will vote up if correct.

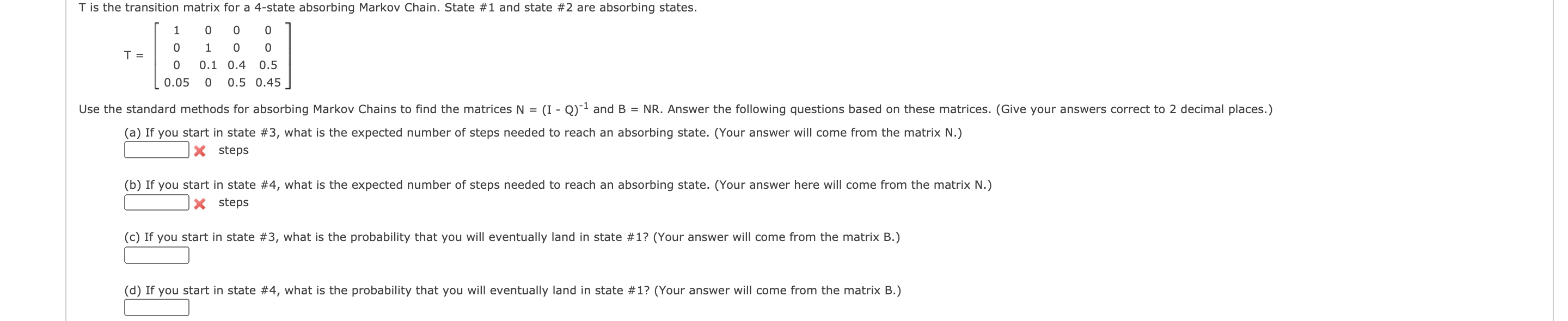
An absorbing Markov Chain has 5 states where states #1 and #2 are absorbing states and the following transition probabilities are known: P3,2=0.3, P3, 3=0.2, P3,5=0.5 P4,1=0.3, P4,3=0.5, P4,4=0.2 P5,1=0.3, P5,2=0.2, P5,4=0.3, P5,5 = 0.2 (a) Let T denote the transition matrix. Compute TS. Find the probability that if you start in state #3 you will be in state #5 after 3 steps. (b) Compute the matrix N = (I - Q)-1. Find the expected value for the number of steps prior to hitting an absorbing state if you start in state #3. (Hint: This will be the sum of one of the rows of N.) steps (c) Compute the matrix B = NR. Determine the probability that you eventually wind up in state #1 if you start in state #4.T is the transition matrix for a 4-state absorbing Markov Chain, State #1 and state #2 are absorbing states. 1 D 0 0 O 1 O 0 D 0.1 0.4 0.5 0.05 0 0.5 0.45 Use the standard methods for absorbing Markov Chains to nd the matrices N = (l - Q)'1 and B = NR. Answer the following questions based on these matrices. (Give your answers correct to 2 decimal places.) (a) If you start in state #3, what is the expected number of steps needed to reach an absorbing state. (Vour answer will come from the matrix N.) x steps (b) If you start in state #4, what is the expected number of steps needed to reach an absorbing state. (Your answer here will come from the matrix N.) x steps (c) If you start in state #3, what is the probability that you will eventually land in state #1? (Your answer will come from the matrix B.) (d) If you start in state #4, what is the probability that you will eventually land in state #1? (Your answer will come from the matrix B.)