Please answer by filling in the question and answer each

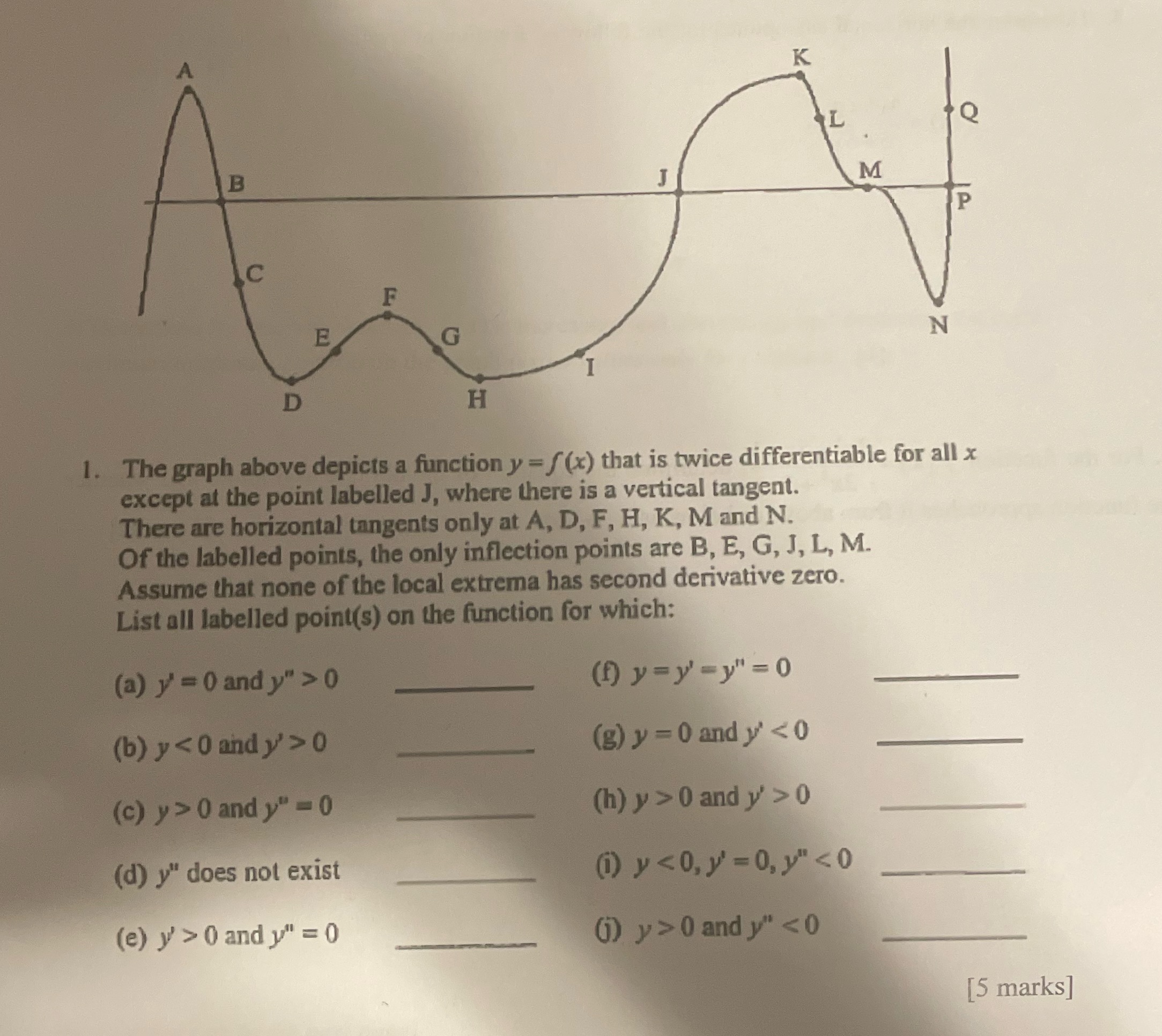
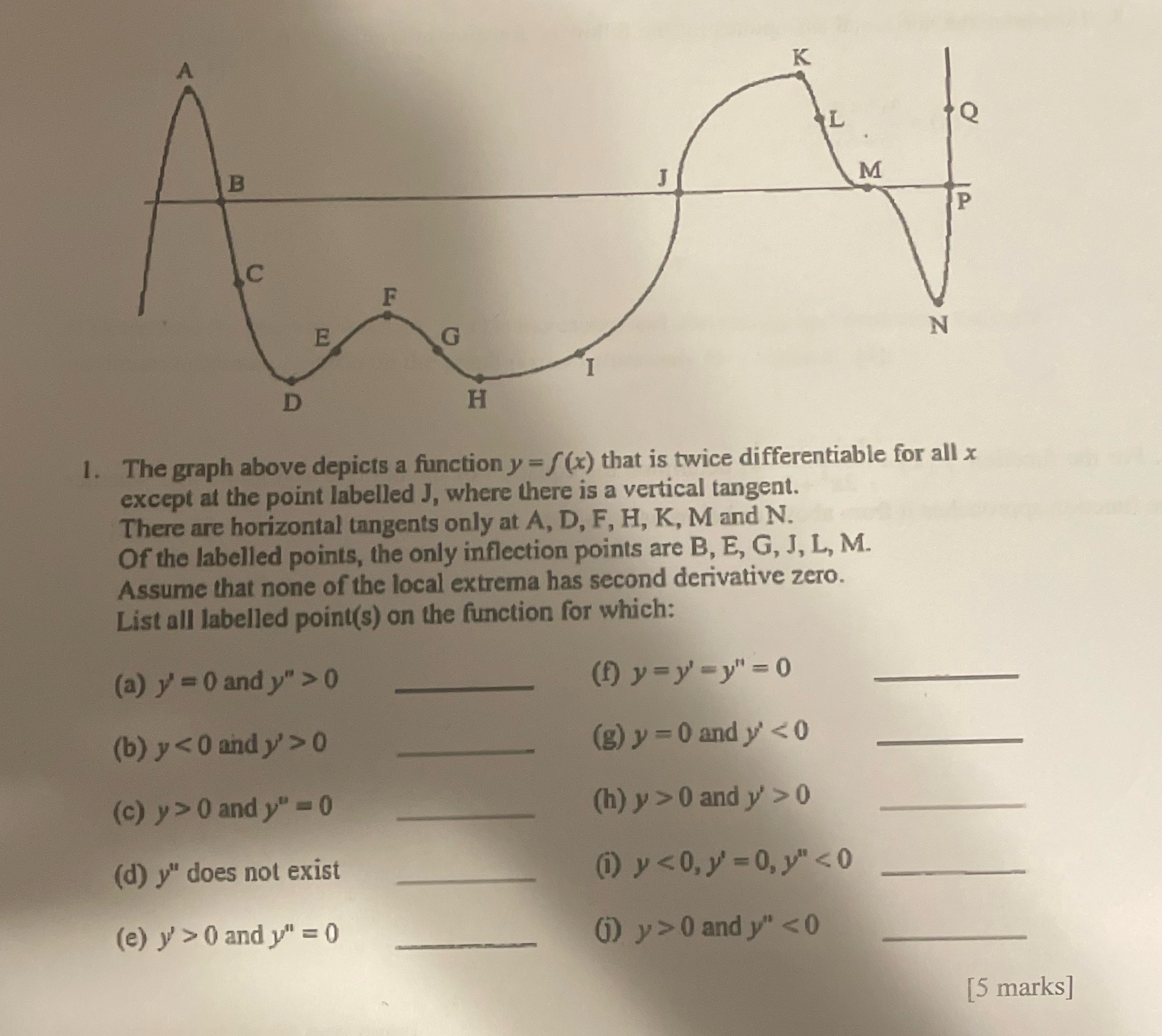
K L B M P G N D H 1. The graph above depicts a function y = f (x) that is twice differentiable for all x except at the point labelled J, where there is a vertical tangent. There are horizontal tangents only at A, D, F, H, K, M and N. Of the labelled points, the only inflection points are B, E, G, J, L, M. Assume that none of the local extrema has second derivative zero. List all labelled point(s) on the function for which: (a) y = 0 and y" > 0 (f) y= y' = y" = 0 (b) y 0 (g) y = 0 and y' 0 and y" = 0 (h) y > 0 and y' > 0 (d) y" does not exist (i) y 0 and y" = 0 () y > 0 and y"