Question: please answer By-hand problem Approximate the above integral using the composite Simp- son rule with 2 intervals of equal length (take n = 4). How
please answer
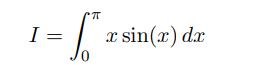
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


