Please Answer, Clear and Concise Answer. Proper Format.

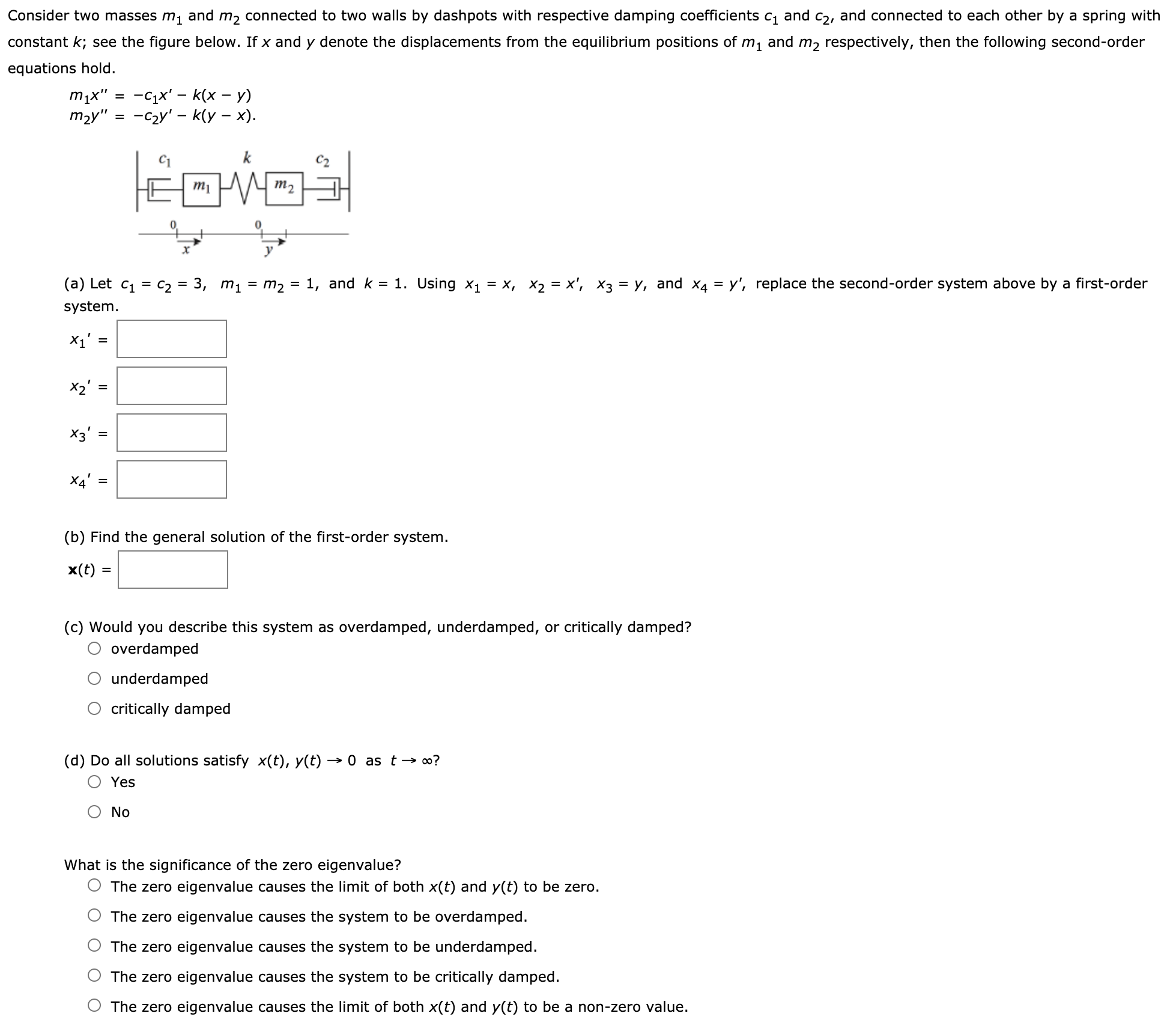
Consider two masses m, and my connected to two walls by dashpots with respective damping coefficients cj and C2, and connected to each other by a spring with constant k; see the figure below. If x and y denote the displacements from the equilibrium positions of m, and m2 respectively, then the following second-order equations hold. mix" = -c1x' - k(x - y) may " = -czy' - k( y - x). m1 m2 (a) Let C1 = C2 = 3, mi = m2 = 1, and k = 1. Using x1 = x, x2 =x', X3 = y, and x4 = y', replace the second-order system above by a first-order system. X1 = X3 XA (b) Find the general solution of the first-order system. x(t) = (c) Would you describe this system as overdamped, underdamped, or critically damped? O overdamped underdamped O critically damped (d) Do all solutions satisfy x(t), y(t) - 0 as t -> co? O Yes O No What is the significance of the zero eigenvalue? The zero eigenvalue causes the limit of both x(t) and y(t) to be zero. The zero eigenvalue causes the system to be overdamped. The zero eigenvalue causes the system to be underdamped. The zero eigenvalue causes the system to be critically damped. The zero eigenvalue causes the limit of both x(t) and y(t) to be a non-zero value