please answer from your own work on a paper providing all steps for good feedback.

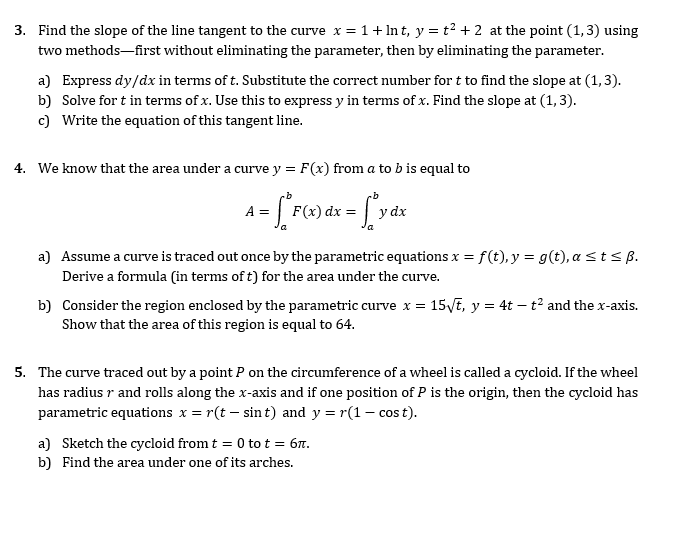
3. Find the slope of the line tangent to the curve 3: = 1 +1nt. y = t2 + 2 at the point (1. 3] using two methodsrst without eliminating the parameter, then by eliminating the parameter. a] Express dyfdx in terms of t. Substitute the correct number for t to nd the slope at (1. 3). b] Solve for t in terms of 1:. Use this to express JF in terms ofx. Find the slope at {1. 3]. c] Write the equation of this tangent line. 4-. We know that the area under a curve 1}! = F{x) from a to h is equal to A=IhF(x]dx=Ibydx a] Assume a curve is traced out once by the parametric equations 3: = f(t], j.- 2 g(t], a E t i: ,8. Derive a Formula [in terms of t} for the area under the curve. b] Consider the region enclosed by the parametric curve A: = 159?, Jr = 4t t2 and the x-axis. Show that the area of this region is equal to I54. 5. The curve traced out by a point P on the circumference of a wheel is called a qrcloid. If the wheel has radius r and rolls along the xaxis and if one position of P is the origin' then the cycloid has parametric equations 3: = r{t sin t} and j.- = r(1 cos t). a] Sketch the cycloid from t = II] to t = n. b] Find the area under one of its arches