please answer

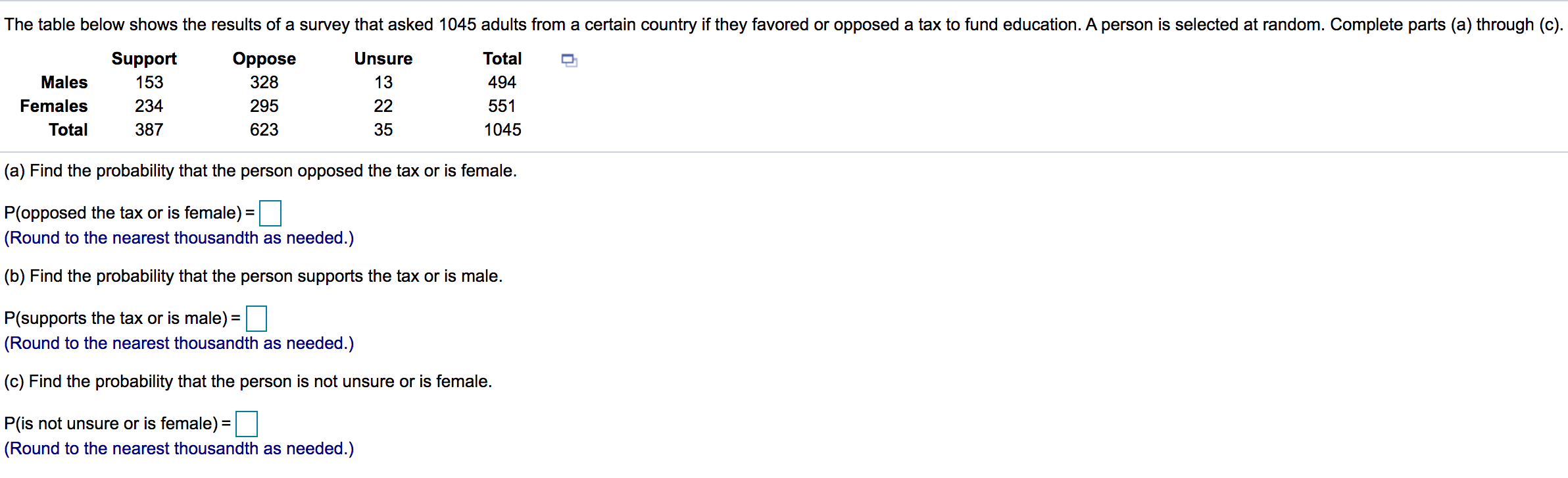
In a random sample of four mobile devices, the mean repair cost was $60.00 and the standard deviation was $11.00. Assume the population is normally distributed and use a t-distribution to find the margin of error and construct a 95% confidence interval for the population mean. Interpret the results. The 95% confidence interval for the population mean u is (]]). (Round to two decimal places as needed.) The margin of error is $. (Round to two decimal places as needed.) Interpret the results. Choose the correct answer below. O A. It can be said that 95% of mobile devices have a repair cost between the bounds of the confidence interval. O B. With 95% confidence, it can be said that the population mean repair cost is between the bounds of the confidence interval. O C. If a large sample of mobile devices are taken approximately 95% of them will have repair costs between the bounds of the confidence interval. O D. With 95% confidence, it can be said that the repair cost is between the bounds of the confidence interval.The table below shows the results of a survey that asked 1045 adults from a certain country if they favored or opposed a tax to fund education. A person is selected at random. Complete parts (a) through (0). Support Oppose Unsure Total D1 Males 153 328 13 494 Females 234 295 22 551 Total 387 623 35 1045 (a) Find the probability that the person opposed the x or is female. P(opposed the tax or is female) = (Round to the nearest thousandth as needed.) (b) Find the probability that the person supports the tax or is male. P(supports the tax or is male) = D (Round to the nearest thousandth as needed.) (0) Find the probability that the person is not unsure or is female. P(is not unsure or is female) = (Round to the nearest thousandth as needed.)