***Please answer in a two-column proof-statements and reasons because it is easier to understand. **Also, please make only one given statement because a lot makes me confused.

It is about lines proportional. The question is in the picture. I have an example of how it looks like in one of the pictures.

This is Theorem 54 that the question is talking about=If a line divides two sides of a triangle proportionally, then it is parallel to the third side.

(Maybe needs to use this reason for to prove? I have no idea, so that's why I need help.

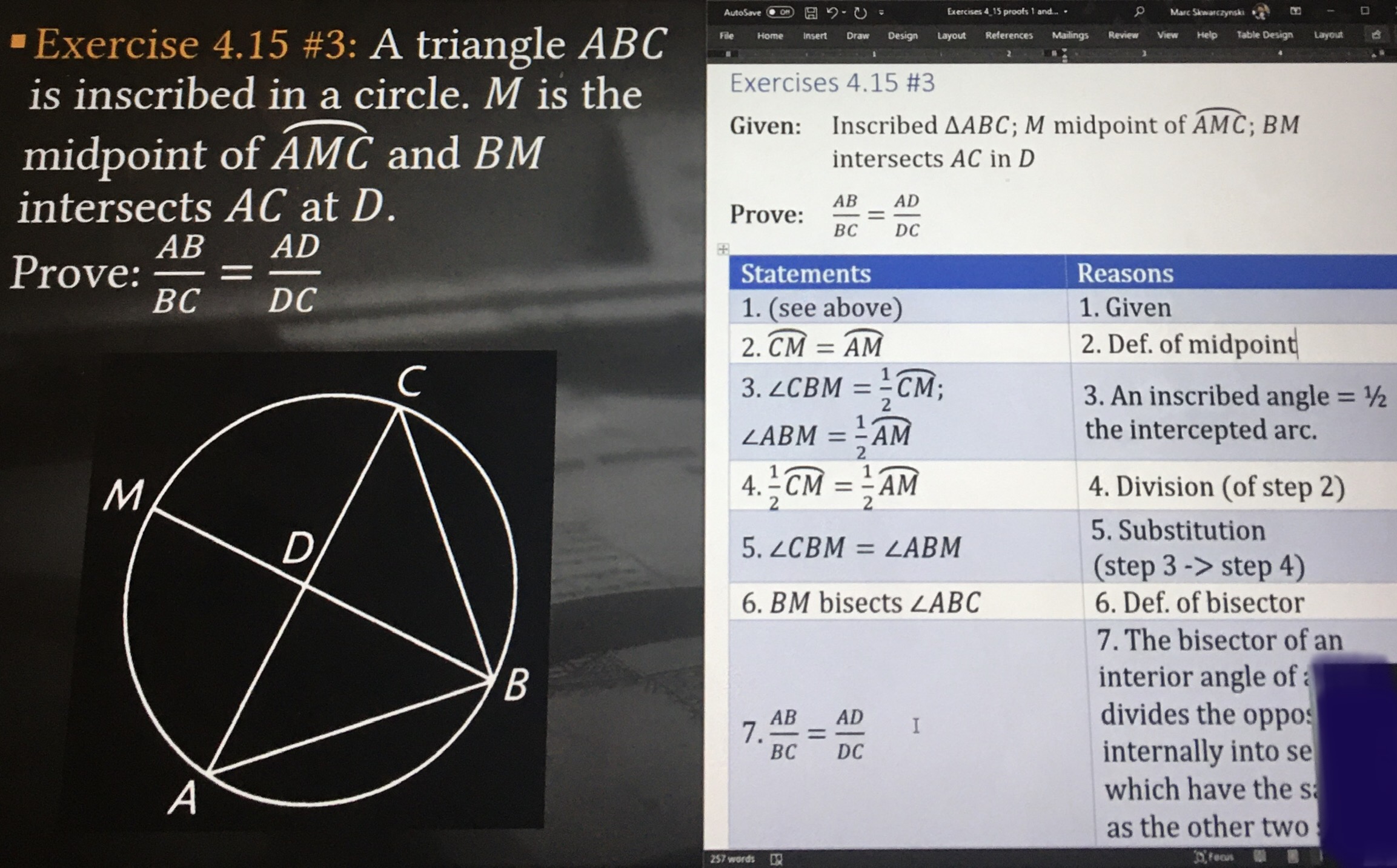
75. D is the midpoint of side BC of triangle ABC and the bisectors of angles ADB and ADC meet AB and AC at E and F respectively. Prove: EF is parallel to BC. (See Theo- rem 54.)AutoSave . O H 9- U D Exercise 4.15 #3: A triangle ABC File Home Insert Draw Design Layout References Mailings Review View Table Design Layout is inscribed in a circle. M is the Exercises 4.15 #3 midpoint of AMC and BM Given: Inscribed AABC; M midpoint of AMC; BM intersects AC in D intersects AC at D. Prove: AB AD AD DC Prove: AB BC DC Statements Reasons BC 1. (see above) 1. Given 2. CM = AM 2. Def. of midpoint C 3. LCBM = -CM; 3. An inscribed angle = 1/2 LABM = - AM 2 the intercepted arc. M 4. - CM = - AM 4. Division (of step 2) D 5. LCBM = LABM 5. Substitution (step 3 -> step 4) 6. BM bisects LABC 6. Def. of bisector 7. The bisector of an B interior angle of 7. AB AD H divides the oppos BC DC internally into se A which have the s as the other two 257 words