Please answer in Lambda calculus. Please and thank you.

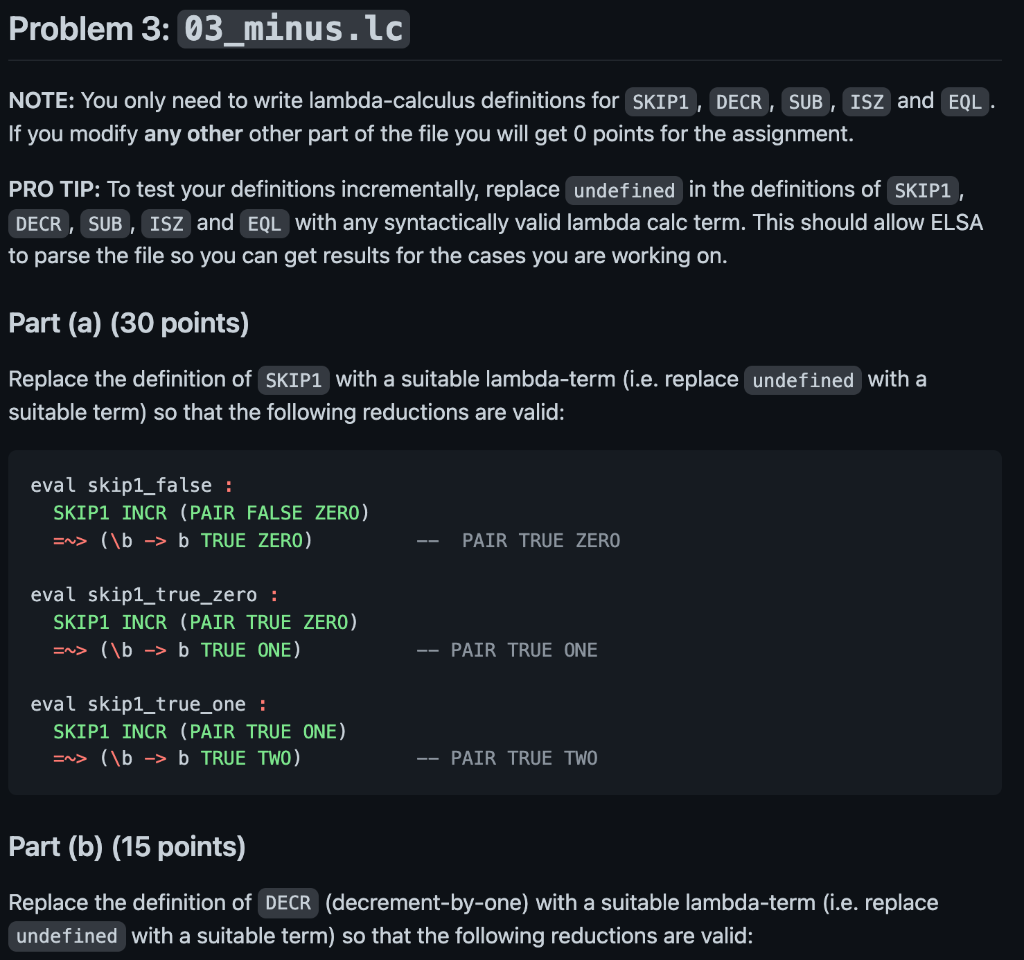
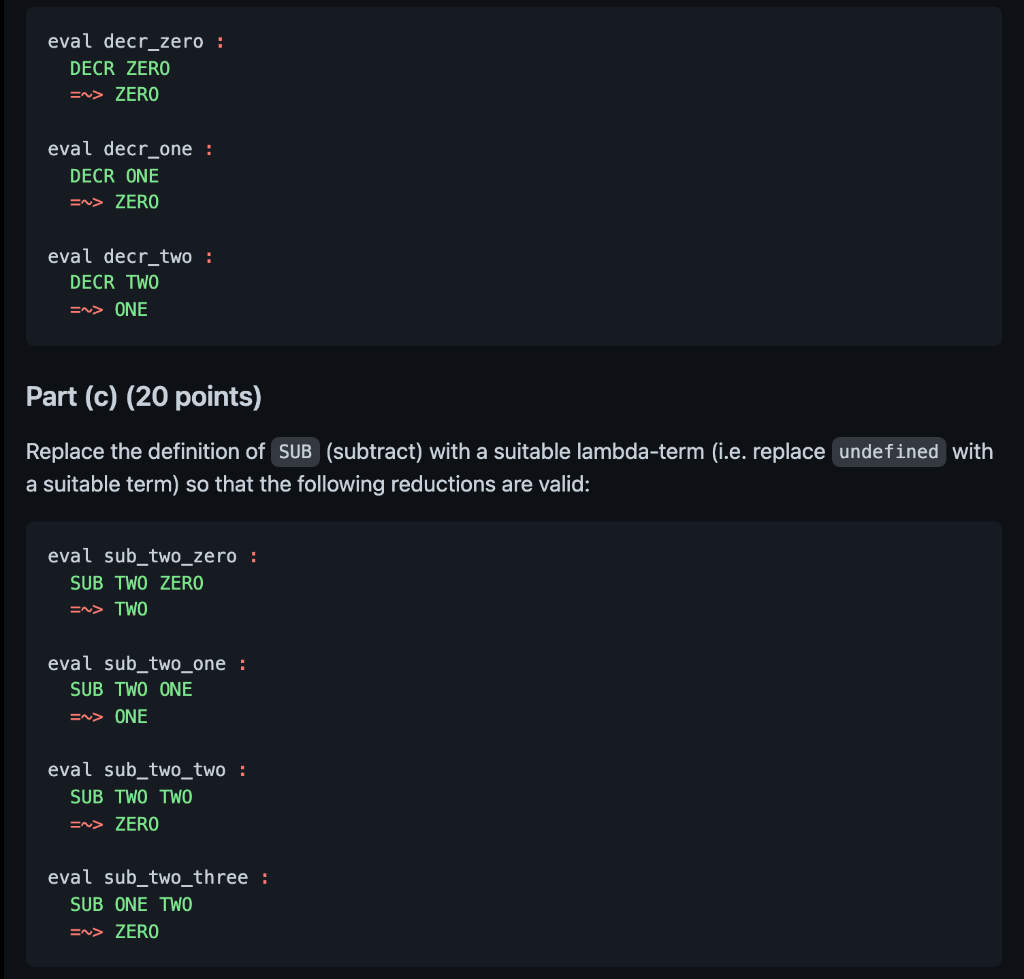
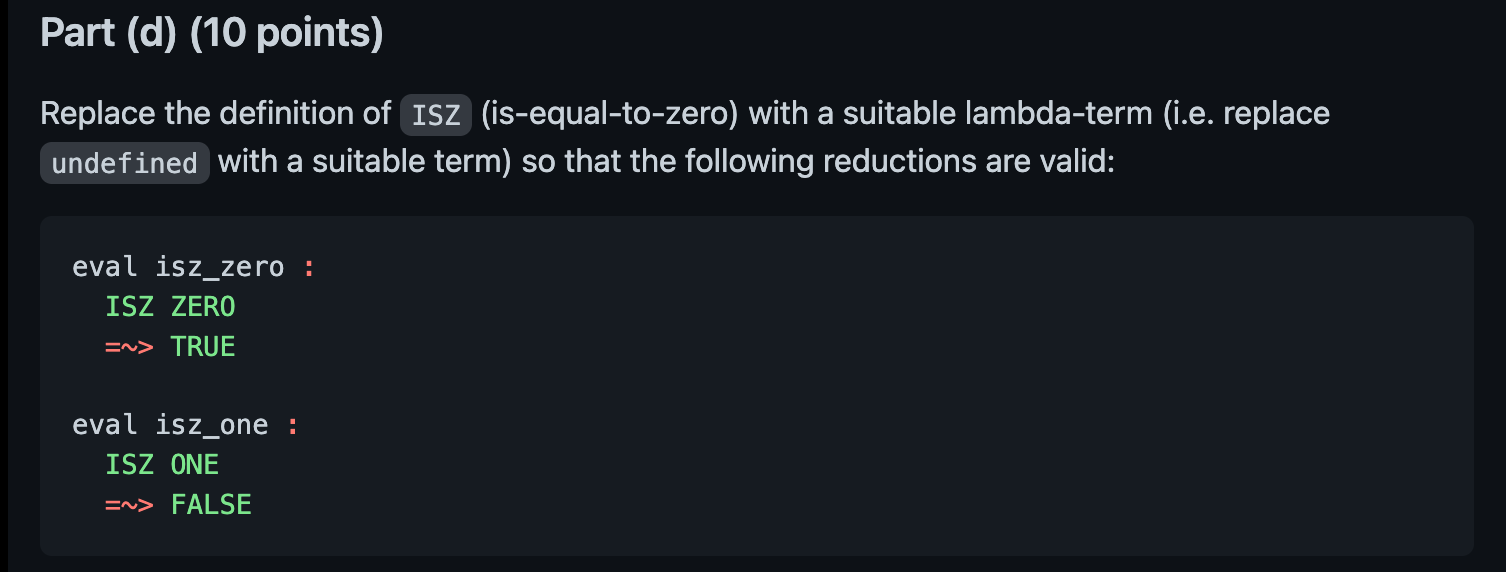
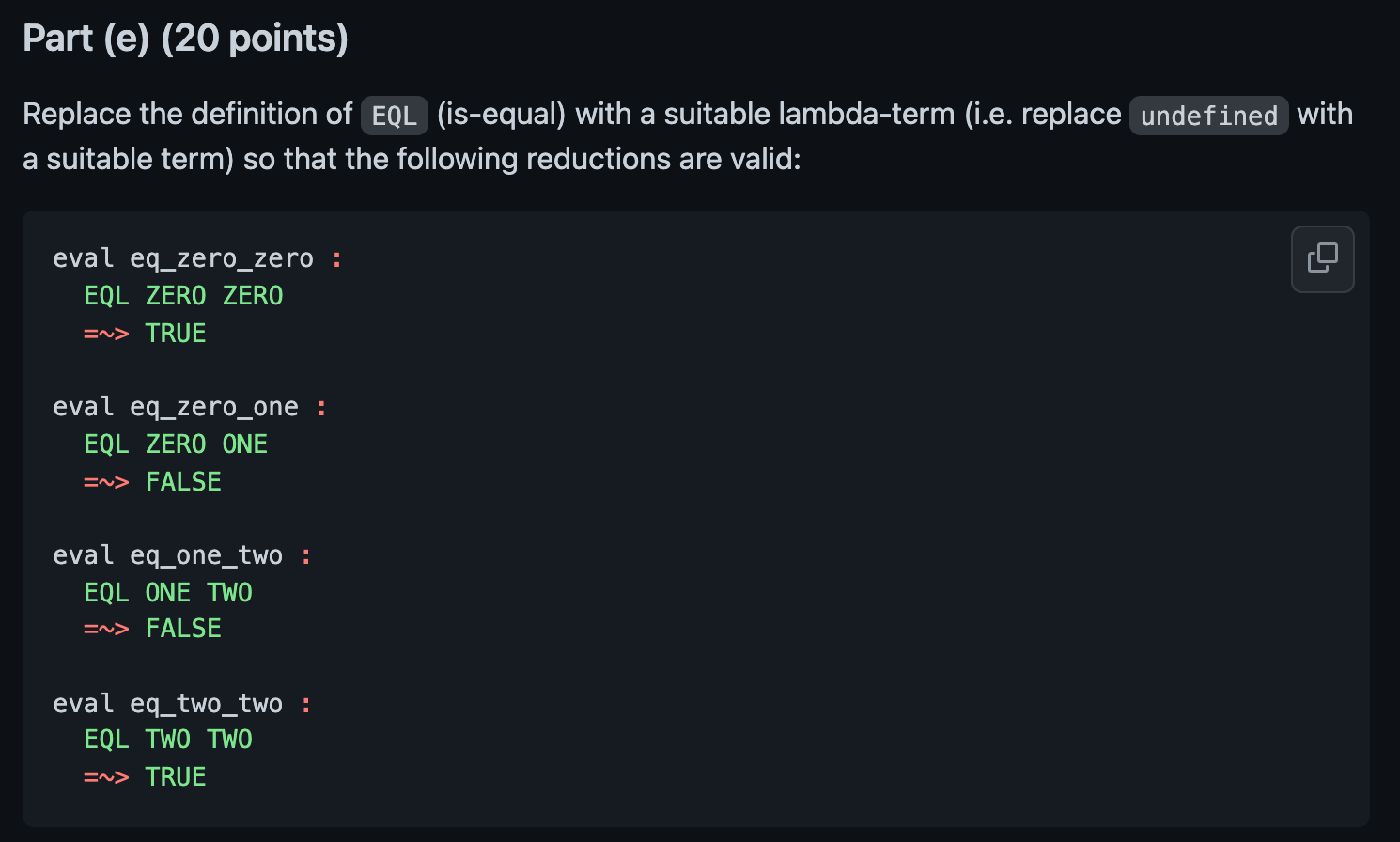
Problem 3: 03_minus.lc NOTE: You only need to write lambda-calculus definitions for SKIP1 , DECR , SUB, ISZ and EQL. If you modify any other other part of the file you will get 0 points for the assignment. PRO TIP: To test your definitions incrementally, replace undefined in the definitions of SKIP1 , DECR , SUB , ISZ and EQL with any syntactically valid lambda calc term. This should allow ELSA to parse the file so you can get results for the cases you are working on. Part (a) (30 points) Replace the definition of SKIP1 with a suitable lambda-term (i.e. replace undefined with a suitable term) so that the following reductions are valid: eval skip1_false : SKIP1 INCR (PAIR FALSE ZERO) =~> (\b -> b TRUE ZERO) PAIR TRUE ZERO eval skip1_true_zero : SKIP1 INCR (PAIR TRUE ZERO) => (\b -> b TRUE ONE) PAIR TRUE ONE eval skip1_true_one : SKIP1 INCR (PAIR TRUE ONE) =~> (\b -> b TRUE TWO) PAIR TRUE TWO Part (b) (15 points) Replace the definition of DECR (decrement-by-one) with a suitable lambda-term (i.e. replace undefined with a suitable term) so that the following reductions are valid: eval decr_zero : DECR ZERO Sv> ZERO eval decr_one : DECR ONE En> ZERO eval decr_two : DECR TWO => ONE Part (c) (20 points) Replace the definition of SUB (subtract) with a suitable lambda-term (i.e. replace undefined with a suitable term) so that the following reductions are valid: eval sub_two_zero : SUB TWO ZERO En> TWO eval sub_two_one : SUB TWO ONE => ONE eval sub_two_two : SUB TWO TWO => ZERO eval sub_two_three : SUB ONE TWO En> ZERO Part (d) (10 points) Replace the definition of IsZ (is-equal-to-zero) with a suitable lambda-term (i.e. replace undefined with a suitable term) so that the following reductions are valid: eval isz_zero : ISZ ZERO =~> TRUE eval isz_one : ISZ ONE =~> FALSE Part (e) (20 points) Replace the definition of EQL (is-equal) with a suitable lambda-term (i.e. replace undefined with a suitable term) so that the following reductions are valid: eval eq_zero_zero : EQL ZERO ZERO => TRUE eval eq_zero_one : EQL ZERO ONE =~> FALSE eval eq_one_two : EQL ONE TWO =~> FALSE eval eq_two_two : EQL TWO TWO =~> TRUE