Please answer it accurately, fully, and be clear to which the answer.

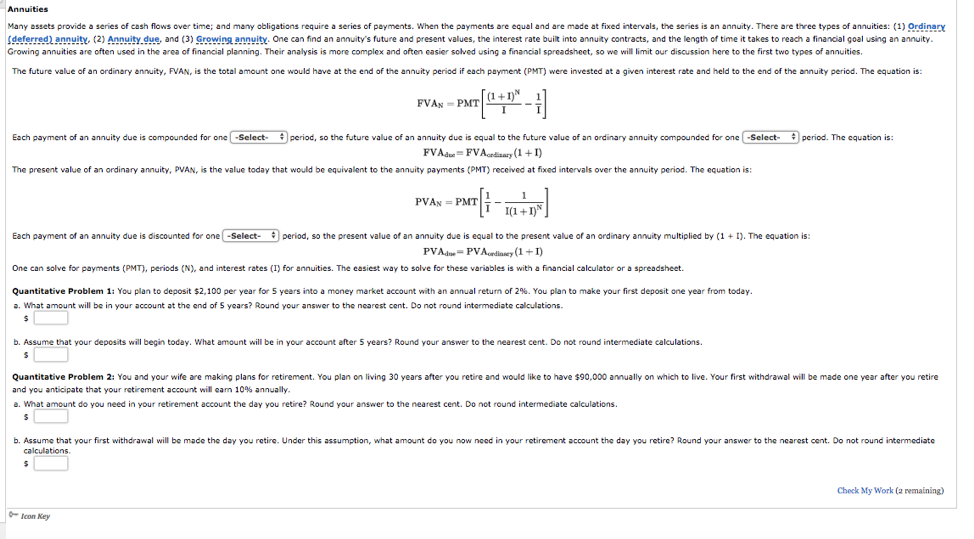
Many assets provide series of cash flows over time; and many obligations require a series of payments. When the payments are equal and are made at fixed intervals, the series is an annuity. There are three types of annuities: (1) Ordinary deferredl annuity, (2) Annuity.due, and (3) Growinaannuity. One can find an annuity's future and present values, the interest rate built into annuity contracts, and the length of time it takes to reach a financial goal using an annuity Growing annuities are often used in the area of financial planning. Their analysis is more complex and often easier solved using a financial spreadsheet, so we will limit our discussion here to the first two types of annuities The future value of an ordinary &nnuity, PAN is the total mount one would have at the end of tennuity period if each payment PT were invested at given interest rte and held to the end of the annuity period. The equation is: IT Each payment of an annuity due is compounded for one Selectperiod, so the future value of an annuity due is equal to the future value of an ardinary annuity compounded for one Select period. The equations The present value of an ordinary annuity, PVAN, is the value today that would be equivalent to the annuity payments (PMT) received at fixed intervals over the annuity period. The equation is: Each payment of an annuity due is discounted for one -Select- period, so the present value of an annuity due is equal to the present value of an ordinary annuity multiplied by (1I). The equation is: One can solve for payments (PMT), periods (N), and interest rates (I) for annuities. The easiest way to solve for these variables is with a financial calculator or a spreadsheet. Quantitative Problem 1: You plan to deposit $2,100 per year for 5 years into a money market account with an annual return of 2%. You plan to make your first deposit one year from today , what amount will be in your account at the end of 5 years? Round your answer to the nearest cent. Do not round intermediate calculations. b. Assume that your deposits will begin today. What amount will be in your account after 5 years? Round your answer to the nearest cent. Do not round intermediate calculations. Quantitative Problem 2: You and your wife are making plans for retirement. You plan on living 30 years after you retire and would like to have $90,000 annually on which to live. Your first withdrawal will be made one year after you retire and you anticipate that your retirement account wil sam 10% annually. a. What amount do you need in your retirement account the day you retire? Round your answer to the nearest cent. Do not round intermediate calculations. b. Assume that your first withdrawal will be made the day you retire. Under this assumption, what amount do you now need in your retirement account the day you retirc? Round your answer to the nearest cent. Do not round intermediate Check My Work (a remaining) Icon Key