PLEASE ANSWER MANUALLY FIRST IN Bellman-Ford's Algorithm TO THE BELOW QUESTION AND THEN IMPLEMENT A PYTHON CODE FOR THE QUESTION AND PLEASE SEND THE PROPER CODE WITH SCREENSHOT OF OUTPUT:

STEP-1 :

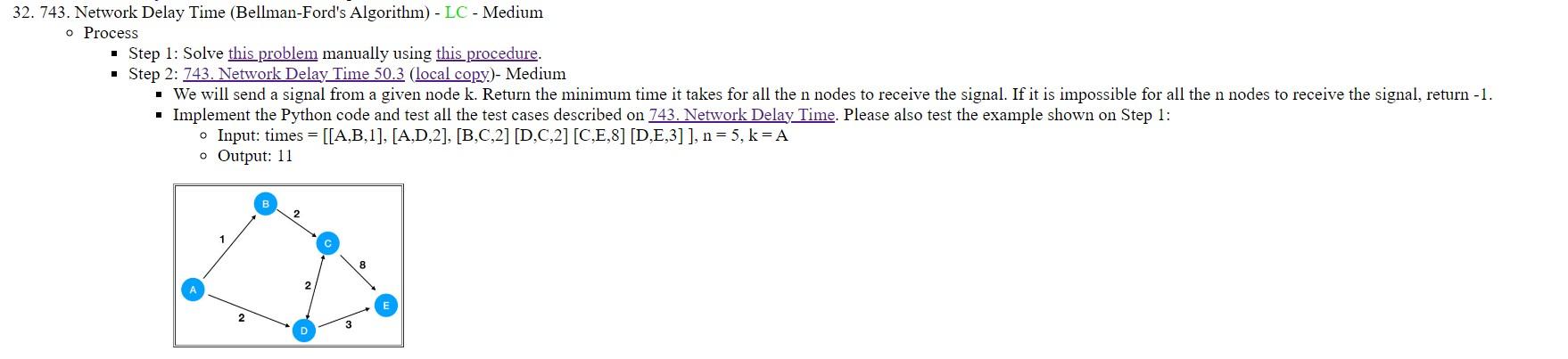
STEP-2 :

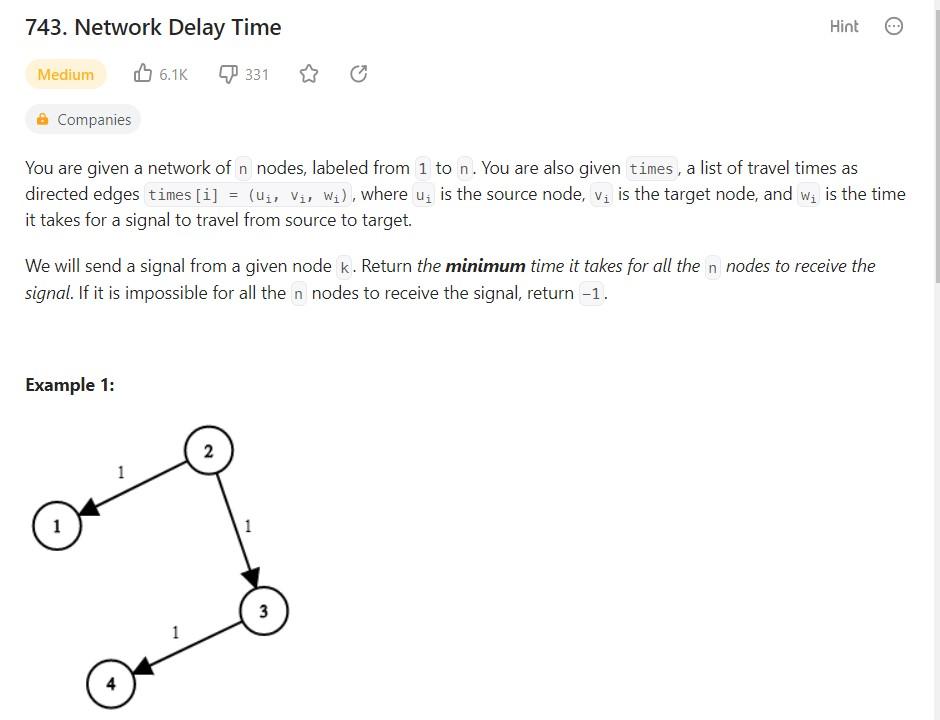
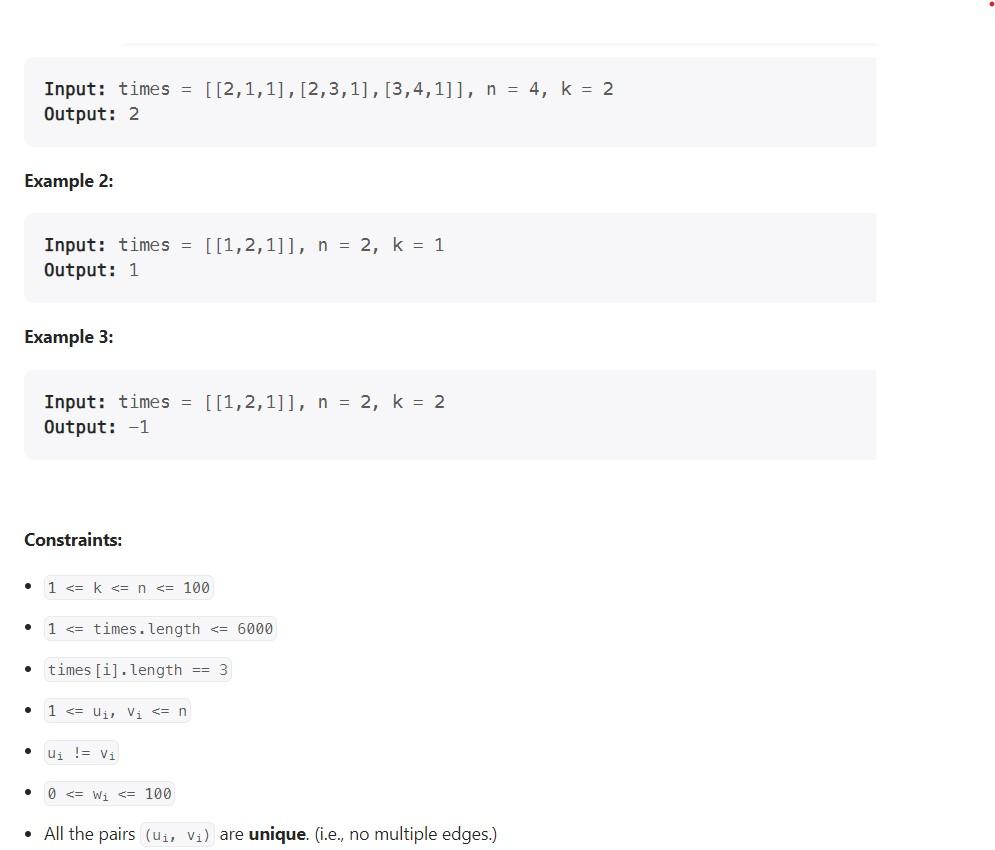
2. 743. Network Delay Time (Bellman-Ford's Algorithm) - LC - Medium - Process - Step 1: Solve this problem manually using this procedure. - Step 2: 743. Network Delay Time 50.3 (local copy)- Medium - Implement the Python code and test all the test cases described on 743 . Network Delay Time. Please also test the example shown on Step 1 : - Input: times =[[A,B,1],[A,D,2],[B,C,2][D,C,2][C,E,8][D,E,3]],n=5,k=A o Output: 11 You are given a network of n nodes, labeled from 1 to n. You are also given a list of travel times as directed edges times [i]=(ui,vi,wi), where ui is the source node, vi is the target node, and is the time it takes for a signal to travel from source to target. We will send a signal from a given node k. Return the minimum time it takes for all the nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return Example 1: Input: times =[[2,1,1],[2,3,1],[3,4,1]],n=4,k=2 Output: 2 Example 2: Input: times =[[1,2,1]],n=2,k=1 Output: 1 Example 3: Input: times =[[1,2,1]],n=2,k=2 Output: 1 Constraints: - 1 times. length =6000 - All the pairs (ui,vi) are unique. (i.e., no multiple edges.)