Please answer only 6.4 part (e) of the question below. Thank you, will upvote correct answer.

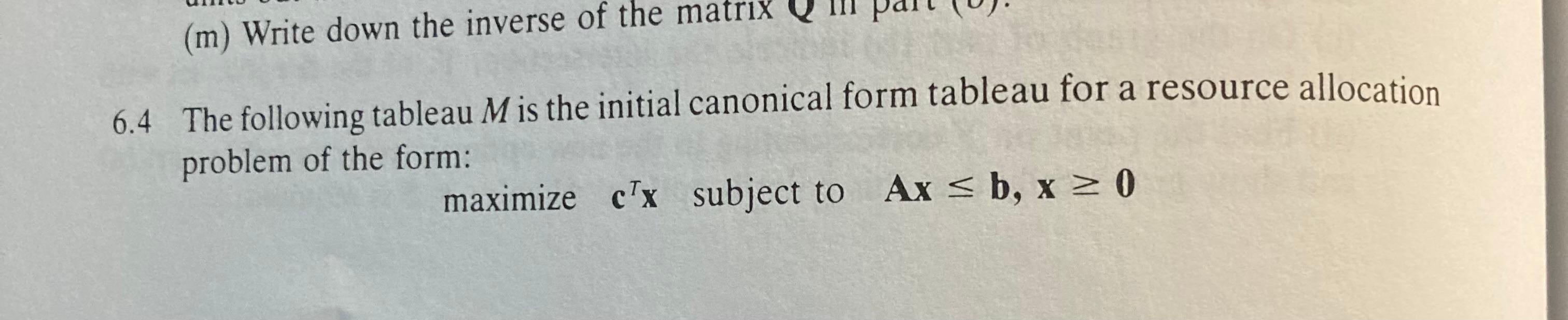
(m) Write down the inverse of the matrix 6.4 The following tableau M is the initial canonical form tableau for a resource allocation problem of the form: maximize ctx subject to Ax s b, x > 0 X X4 S. X -6 X2 - 1 X 3 4 S2 0 S3 0 -5 0 M = 0 20 10 5 2 1 1 1 0 1 1 2 1 1 1 0 1 0 0 0 1 0 0 0 1 Here, x, denotes the amount of product i produced and s, is the slack variable for resource i. For example, product 2 sells for 1 and uses 1 unit each of resource 1 and resource 3. The optimal tableau M* is x X4 Si S3 X2 0 X3 7 S2 5 0 0 1 55 5 5 5 uruu Blood M* = 0 0 1 0 -1 1 -2 1 1 0 1 0 1 0 0 - 1 1 0 - 1 -1 1 (a) Find a matrix Q such that M* = QM. (b) What is the minimum amount we should charge for 8 units of resource 2 so the total revenue from selling these 8 units and selling products will not be less than 55? (c) What is the new optimal vector x* if only 4 units of resource 3 are available instead of the original 5? (d) What is the new optimal vector x* if 8 units of resource 3 are available instead of the original 5? (e) Give a range in which the selling price of product 1 can vary without changing the optimal basic sequence. (f) What is the smallest amount by which the selling price of product 3 should be increased so that product 3 would be produced in an optimal production program? (g) What is the new optimal production program if the selling price of product 4 increases to 6? (m) Write down the inverse of the matrix 6.4 The following tableau M is the initial canonical form tableau for a resource allocation problem of the form: maximize ctx subject to Ax s b, x > 0 X X4 S. X -6 X2 - 1 X 3 4 S2 0 S3 0 -5 0 M = 0 20 10 5 2 1 1 1 0 1 1 2 1 1 1 0 1 0 0 0 1 0 0 0 1 Here, x, denotes the amount of product i produced and s, is the slack variable for resource i. For example, product 2 sells for 1 and uses 1 unit each of resource 1 and resource 3. The optimal tableau M* is x X4 Si S3 X2 0 X3 7 S2 5 0 0 1 55 5 5 5 uruu Blood M* = 0 0 1 0 -1 1 -2 1 1 0 1 0 1 0 0 - 1 1 0 - 1 -1 1 (a) Find a matrix Q such that M* = QM. (b) What is the minimum amount we should charge for 8 units of resource 2 so the total revenue from selling these 8 units and selling products will not be less than 55? (c) What is the new optimal vector x* if only 4 units of resource 3 are available instead of the original 5? (d) What is the new optimal vector x* if 8 units of resource 3 are available instead of the original 5? (e) Give a range in which the selling price of product 1 can vary without changing the optimal basic sequence. (f) What is the smallest amount by which the selling price of product 3 should be increased so that product 3 would be produced in an optimal production program? (g) What is the new optimal production program if the selling price of product 4 increases to 6