PLEASE ANSWER ONLY QUESTIONS ASKED: E THRU I

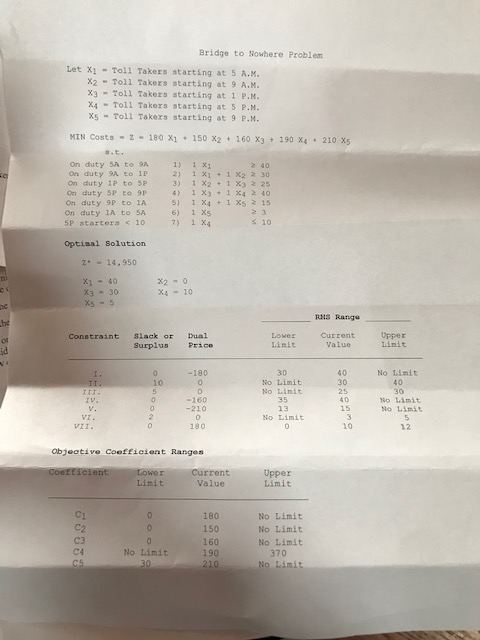
Part Two: Interpretation 3. This part of the examination requires you to interpret the output from a proper setup of a "Bridge to Nowhere" problem. The problem is printed below, and it is followed by a copy of the computer output. The "Bridge to Nowhere in rural Alaska is designed as a monument to Senator Dolt, who represented Alaska (and a number of his close corporate friends) in the United States Senate. Although the bridge figures to serve at most 300 people a day, it has been optimistically designed with 50 toll booths. The plan for the operation of the toll system calls for the number of toll takers to vary over the course of a typical day: Minimum # Toll Takers Time 5 AM 9 AM 1 P.M. SP.M 9 P.M. 1 A.M. to to to to to to 9A.M. 1P.M. SP.M. 9 P.M. 1A.M. 5 A.M. Toll takers work 8 hour shifts, and shifts start at 5 A.M., 9 A.M., 1 P.M.. 5 P.M. and 9 P.M. No more than 10 toll takers can start at 5PM The cost of toll takers ranges from 150 to 210 dollars per 8 hour shift, depending upon the starting time of the shift: Starting Time Cost per Toll Taker 180 5 A.M. 9 A.M 1 P.M. SP.M. 9 P.M. 150 160 190 210 The goal is to determine a work schedule that minimizes the total daily cost for toll takers, while meeting the minimum requirements listed above. Bridge to Nowhere Problem Let Xi - Toll Takers starting at 5 A.M. X2 - Toll Takers starting at 9 A.M. X -Toll Takers starting at 1 P.M. X4 - Toll Takers starting at 5 P.M. X5 - Toll Takers starting at 9 P.M. MIN Costa - 2 - 180 X1 + 150 X2 + 160 X3 + 190 X 210 X5 On duty to SA On duty to 1P On duty IP to 5P On duty SP to 9p On duty 9p to IA On duty 1A to SA 5P starters 10 1) 1 X1 40 2) 1 x + 1 X2 230 3) 1X2 + 1 X3 25 4) 1 X3 + 14 240 5) 1 X4 + 1 XS 15 6) 1 Xs 7) 1 X4 Optimal solution z. - 14.950 X1 - 40 X3 - 30 X - 5 X2 - 0 X4 - 10 BUS Range Constraint Slack or Surplus Dual Price Lower Current Value Upper Limit -180 No Limit No Limit No Limit 25 - 160 -210 To Limit No Limit No Limit VII. 180 Objective Coefficient Ranges Coefficient Lower Limit Current Value Upper Limit 180 150 160 No Limit No Limit No Limit 370 No Limit No Limit 190 210 The point of an examination of this kind is not just to get the correct numerical answer. Rather to demonstrate your knowledge of the techniques we have learned in . Many of the questions below are about sensitivity analysis. You are expected to use the appropriate technique, and to use it properly. Further, it is your responsibility to clearly state what technique you have used and how you have used it. The correct numerical answer, without demonstrated knowledge of the appropriate technique, is not adequate. E. Would the optimal work schedule be the same if the wage for a toll taker starting at 5 P.M. increased to 200 per shift? Explain. F. What is the minimum change in the cost of toll takers starting at 5 P.M. that would produce al change in the optimal work schedule? Explain. G. How would the result be affected if 12 toll takers were allowed to start at 5 P.M.? Explain. H. How would the result be affected in 14 toll takers were allowed to start at 5 P.M.? Explain. I How would one go about determining the optimal value of the objective function if the right hand sides of the first three constraints were all increased by 2? Do not do it, just explain how one would proceed. Part Two: Interpretation 3. This part of the examination requires you to interpret the output from a proper setup of a "Bridge to Nowhere" problem. The problem is printed below, and it is followed by a copy of the computer output. The "Bridge to Nowhere in rural Alaska is designed as a monument to Senator Dolt, who represented Alaska (and a number of his close corporate friends) in the United States Senate. Although the bridge figures to serve at most 300 people a day, it has been optimistically designed with 50 toll booths. The plan for the operation of the toll system calls for the number of toll takers to vary over the course of a typical day: Minimum # Toll Takers Time 5 AM 9 AM 1 P.M. SP.M 9 P.M. 1 A.M. to to to to to to 9A.M. 1P.M. SP.M. 9 P.M. 1A.M. 5 A.M. Toll takers work 8 hour shifts, and shifts start at 5 A.M., 9 A.M., 1 P.M.. 5 P.M. and 9 P.M. No more than 10 toll takers can start at 5PM The cost of toll takers ranges from 150 to 210 dollars per 8 hour shift, depending upon the starting time of the shift: Starting Time Cost per Toll Taker 180 5 A.M. 9 A.M 1 P.M. SP.M. 9 P.M. 150 160 190 210 The goal is to determine a work schedule that minimizes the total daily cost for toll takers, while meeting the minimum requirements listed above. Bridge to Nowhere Problem Let Xi - Toll Takers starting at 5 A.M. X2 - Toll Takers starting at 9 A.M. X -Toll Takers starting at 1 P.M. X4 - Toll Takers starting at 5 P.M. X5 - Toll Takers starting at 9 P.M. MIN Costa - 2 - 180 X1 + 150 X2 + 160 X3 + 190 X 210 X5 On duty to SA On duty to 1P On duty IP to 5P On duty SP to 9p On duty 9p to IA On duty 1A to SA 5P starters 10 1) 1 X1 40 2) 1 x + 1 X2 230 3) 1X2 + 1 X3 25 4) 1 X3 + 14 240 5) 1 X4 + 1 XS 15 6) 1 Xs 7) 1 X4 Optimal solution z. - 14.950 X1 - 40 X3 - 30 X - 5 X2 - 0 X4 - 10 BUS Range Constraint Slack or Surplus Dual Price Lower Current Value Upper Limit -180 No Limit No Limit No Limit 25 - 160 -210 To Limit No Limit No Limit VII. 180 Objective Coefficient Ranges Coefficient Lower Limit Current Value Upper Limit 180 150 160 No Limit No Limit No Limit 370 No Limit No Limit 190 210 The point of an examination of this kind is not just to get the correct numerical answer. Rather to demonstrate your knowledge of the techniques we have learned in . Many of the questions below are about sensitivity analysis. You are expected to use the appropriate technique, and to use it properly. Further, it is your responsibility to clearly state what technique you have used and how you have used it. The correct numerical answer, without demonstrated knowledge of the appropriate technique, is not adequate. E. Would the optimal work schedule be the same if the wage for a toll taker starting at 5 P.M. increased to 200 per shift? Explain. F. What is the minimum change in the cost of toll takers starting at 5 P.M. that would produce al change in the optimal work schedule? Explain. G. How would the result be affected if 12 toll takers were allowed to start at 5 P.M.? Explain. H. How would the result be affected in 14 toll takers were allowed to start at 5 P.M.? Explain. I How would one go about determining the optimal value of the objective function if the right hand sides of the first three constraints were all increased by 2? Do not do it, just explain how one would proceed