please answer questions b and c

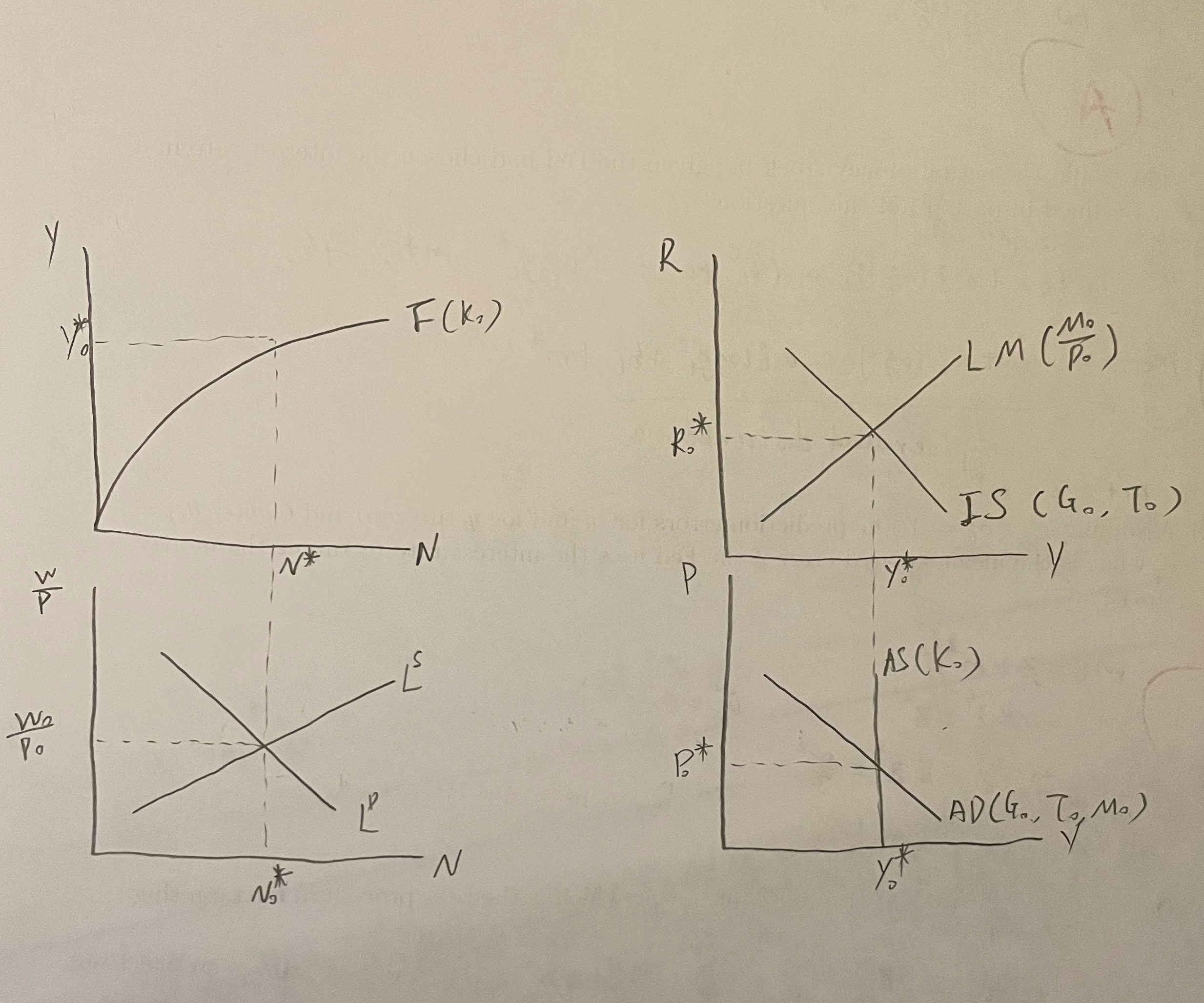
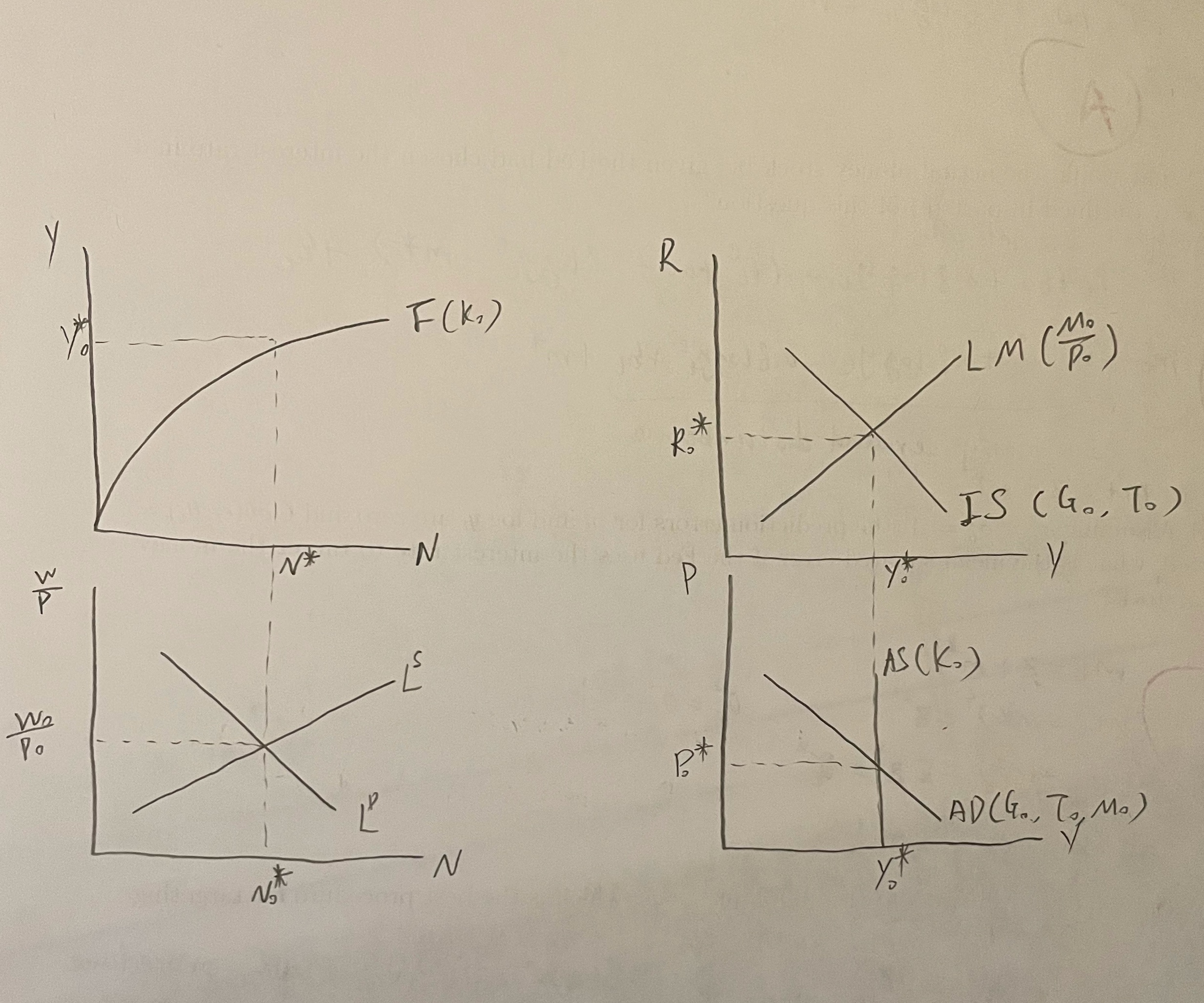
Consider the following Classical Model, Y = C( Y - T, R) + I( Y, R) + G, M P = L(Y, R). Y = F( N, K ), W FN = P' Ns h ( W (a) Using this model, analyze by showing graphically the effect on all the endogenous variables of an expansionary monetary policy (Find dy ap dw/P dN dR aM ' dM' dM ' dM' dM ) b) Again, using the above classical model, substitute C = C(Y - T, R, M/P) for the original consumption function in the IS curve. Assume C3 > 0, the idea here is that greater real wealth leads to more consumption. With this modification, does the classical model continue to have the property called "neutrality of money"? Does it continue to dichotomize? (To answer this question, you must analyze graphically a decrease in the growth rate of money on all the endogenous variables. What happens to real money holdings and investment spending given a decrease in the growth rate of money?) c) Does the property called "neutrality of money" imply that a monetary economy would have the same output if it were a barter economy with no money? d) Suppose that an economy's production function is initially Y = 3/0.4, but then a technological innovation shifts it to Y = 6/0.4. Also, assume the labor supply behavior is given by N = 30W/P. Determine algebraically the equilibrium values of N* and Y* before and after the technological improvement. Represent the change graphically, and using the classical model show what would happen to R, P, W/P, Y and N.