Question: A and B are real nonzero 3 3 matrices and satisfy the equation 1. Prove that if B is orthogonal then A is antisymmetric.

A and B are real nonzero 3 × 3 matrices and satisfy the equation

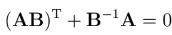
(AB)T + B-A = 0

1. Prove that if B is orthogonal then A is antisymmetric.
2. Without assuming that B is orthogonal, prove that A is singular (i.e., its determinant
vanishes).

(AB)T + B-A = 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Matrix Definitions and Properties of Determinants Orthogonal Matrices A matrix is said to be ort... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

If ∫∞ f(x) dx- is convergent and a and b are real numbers, show that f) dx + r) dx = f) dx + fx) dx

Prove that if Q is nonsingular matrix with Qt = Q1, then Q is orthogonal.

Prove that if f is absolutely integrable on (l, ), then lime, f(x" ) dx=0.

In the real number system the equation a2 = 1 has exactly two solutions. Find at least eight different 3 3 matrices that satisfy the equation A2 = I3.

Let F = f , where f (x, y) = sin(x - 2y). Find curves C 1 and C 2 that are not closed and satisfy the equation. F dr = 1 (a) (b) |F dr = 0

(Show that the matrix Q = In & XX0 X &1 X0 (see Section 10.3) is nondiagonal, singular, and of rank n & k & 1. (Hints: Verify that the rows of Q satisfy the k 1 constraints implied by QX = 0. If Q...

4. Use the data from Table 6.1 to calculate annual growth rates of GDP per capita for each country listed over the period 1950-2006. [Note: The annual growth rate z will satisfy the equation (1 +...

4. Use the data from Table 6.1 to calculate annual growth rates of GDP per capita for each country listed for the years 1870, 1950, and 2016. [Note: The annual growth rate z will satisfy the equation...

In this exercise, we explore the concept o f marginal rates of substitution (and, in part B, its relation to utility functions) further. A: Suppose I own 3 bananas and 6 apples, and you own 5 bananas...

Suppose the Swiss federal government in Bern proposed building a high-speed train line from Zurich to Geneva. Instead to taking the normal 2.5 hours to get from one city to the other, the new line...

As a Teller, you will be accountable for meeting customers' financial transaction needs. In addition to this, it is expected that you will provide exceptional customer service and contribute to...

What are the magnitudes and directions of each of the following position vectors? When reporting a direction, make sure you give the amount of rotation, the direction of rotation, and the starting...

For each situation, select the appropriate reporting treatment from the list below ( consider each event to be material ) : As an unusual gain or lossAs a prior period adjustmentAs a change in...

Design the logic circuit that squares two four-bit numbers. Find and show the output values that will occur if the number (1101) _2 is applied to the logic circuit that squares two four-bit numbers...

1. Bank holding companies can issue common stock to raise equity capital? True or False 2 - Between 1/2008 and 12/2009 the monetary base of the Federal Reserve System increased from $1 trillion US....

8. Choose the double integral that is equivalent to the 4 4 y + 1 x4 + 1 2 integral dx dy. 0. (a) 4 y + 1 dy dx x4 + 1 Va (b) 4 y + 1 dy dx + 1 (c) 4 y + 1 x4 + 1 dy dx 0, (d) .2 4 y + 1 dy dx 0. x4...

1. Which institution has the most benefits for a checking account? 2. What three things would influence your decision the most when looking for a checking account? 3. Why would a financial...

When preparing a scatter diagram, the estimated line of cost behavior is drawn on a scatter diagram to show the relation between: When preparing a scatter diagram, the estimated line of cost behavior...

Write out the details of the proof of Theorem 2.1.3.

Show that if two n n matrices A and B have a common eigenvector x (but not necessarily a common eigenvalue), then x will also be an eigenvector of any matrix of the form C A + b.

Let A be a nonsingular matrix. Show that det(A-1) = 1 / det(A)

11.44. A recent article6 used multiple regression to predict attitudes toward homosexuality. The researchers found thatthe effect ofnumber ofyears of education on a measure of tolerance toward...

11.38. In about 200 words, explain to someone who has never studied statistics what multiple regression does and how it can be useful.

11.33. Refer to the student data file you created in Exercise 1.12. For variables chosen by yourinstructor, fit a multiple regression model and conduct descriptive and inferential statistical...