Please answer the one you can

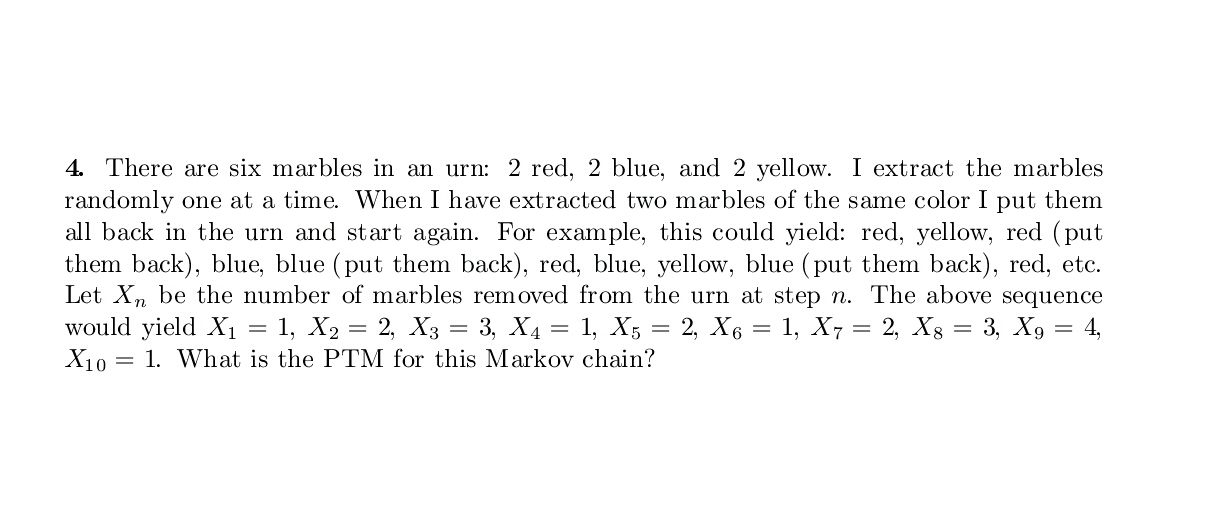
4. There are six marbles in an urn: 2 red, 2 blue, and 2 yellow. I extract the marbles randomly one at a time. When I have extracted two marbles of the same color I put them all back in the urn and start again. For example, this could yield: red, yellow, red (put them back), blue, blue (put them back), red, blue, yellow, blue (put them back), red, etc. Let X,, be the number of marbles removed from the urn at step n. The above sequence wouldyielXm = 1, X2: 2, X3: 3, X4: 1, X5: 2, X6: 1, X7: 2, X8: 3, X9: 4, X10 = 1. What is the PTM for this Markov chain? 6. A stock analyst has discovered that if IBM's share price goes up two days in a row, it will go down the third day with probability 0.6. Similarly, if it goes down two days in a row, it will go up the third day with probability 0.6. If it goes up then down or down then up on any two consecutive days, it will go up (or down) on the third day with probability 0. 5. Turn this into a Markov chain. Describe the states and write down the PTM. Assume the price either goes up or down and never remains the same. 9. A game works as follows. Clock A's alarm sounds once at a random time uniformly distributed over the next hour. Clock B rings according to an I-[PP with rate 10 per hour. Before play starts, you announce a time t between 0 and 1 hour at which time you will quit the game. If clock A has not rung by time t, I will pay you $1 for every ring of clock B up to time t and the game ends. If clock A rings before time it, you must pay me $5 and the game ends. What quitting time t maximizes your expected winnings? What are your expected winnings with this optimal strategy? 5. Our underlying probability space all semester has been the unit interval (2 = (0, 1). Explain how to use a number a: drawn uniformly from Q to construct a realization of: (a) A Markov chain X0, X1, X2, . . . where X9 is drawn uniformly from the states {1, 2, 3} 0.5 0.5 0 and Whose PTM is P = 0.25 0.25 0.5 1 0 0 (b) An iid sequence of mean 2 exponential random variables