Please answer the part EFGH. thanks!

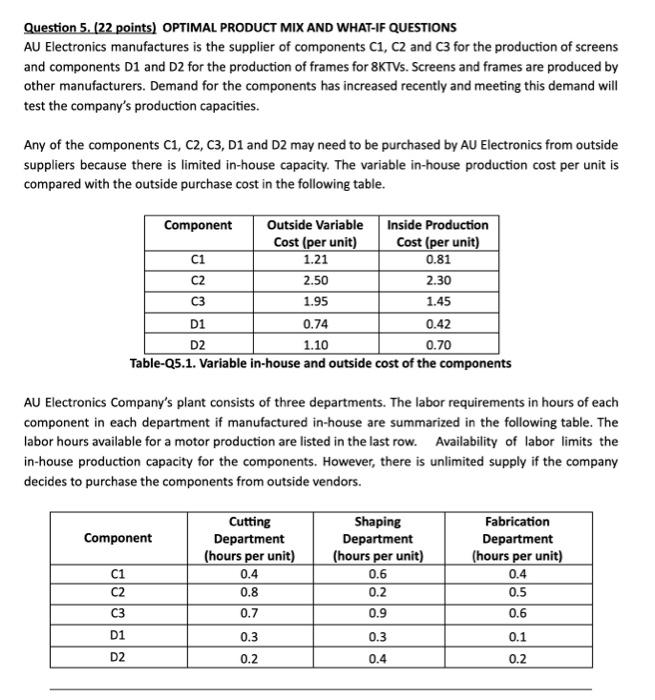
Question 5. (22 points) OPTIMAL PRODUCT MIX AND WHAT-IF QUESTIONS AU Electronics manufactures is the supplier of components C1, C2 and C3 for the production of screens and components D1 and D2 for the production of frames for KTVs. Screens and frames are produced by other manufacturers. Demand for the components has increased recently and meeting this demand will test the company's production capacities. Any of the components C1, C2, C3, D1 and D2 may need to be purchased by AU Electronics from outside suppliers because there is limited in-house capacity. The variable in-house production cost per unit is compared with the outside purchase cost in the following table. Component Outside Variable Inside Production Cost (per unit) Cost (per unit) C1 1.21 0.81 C2 2.50 2.30 C3 1.95 1.45 D1 0.74 0.42 D2 1.10 0.70 Table-Q5.1. Variable in-house and outside cost of the components AU Electronics Company's plant consists of three departments. The labor requirements in hours of each component in each department if manufactured in-house are summarized in the following table. The labor hours available for a motor production are listed in the last row. Availability of labor limits the in-house production capacity for the components. However, there is unlimited supply if the company decides to purchase the components from outside vendors. Component Cutting Department (hours per unit) 0.4 0.8 Shaping Department (hours per unit) 0.6 0.2 0.9 C1 C2 Fabrication Department (hours per unit) 0.4 0.5 0.6 c3 0.7 D1 0.3 0.3 0.1 D2 0.2 0.4 0.2 Capacity (total available labor hours) 250 325 175 Table-25.2. Labor hour requirements per unit produced and monthly available labor hours at each department The company is already in a contract with clients for the next month. The confirmed number of components to be delivered are given in Table-05-3. These numbers show the number of components the company has committed to sell and is the minimum demand AU Electronics must meet. Component C1 C2 C3 D1 D2 Minimum number of products to be sent to clients next month 200 250 150 45 50 Table-25.3. Confirmed demand for next month You are asked to determine the optimal product mix (i.e., the monthly number of each product type to be provided) that minimizes AU Electronics' production total production and purchasing costs for next month. You will formulate a linear programming model to determine the optimal solution using Excel Solver 1 NOTE: SHOW ALL YOUR WORK. a) (3 points) What are the decision variables? How many decision variables are there? Clearly explain the decision variables in English and provide the mathematical notation used in the algebraic formulation of the decision problem. Decision variables: Let C1(In)- number of C1 component produced in house C1 (out)- number of Ci component purchasing from outside C2 (In)- number of C2 component produced in house C2 (out)- number of C2 component purchasing from outside C3 (In)- number of C3 component produced in house C3 (out)- number of C3 component purchasing from outside D1 (In)- number of D1 component produced in house D1 (out)- number of D1 component purchasing from outside D2 (In)- number of D2 component produced in house D2 (out)- number of D2 component purchasing from outside There are 10 decision variables. b) (2 points) What is the objective function? Clearly explain the objective function in English and provide the mathematical formulation. To minimise the cost of production in house and purchasing from outside as well. So, objective function Z= Min(1.21 C1(out) +0.81 C1 (In) + 2.5 C2 (out)+ 2.30 C2 (In)+ 1.95 C3(Out) + 1.45 C3(In) + 0.74 D1(out) +0.42 D1 (In)+1.10 D2(out)+ 0.7 D2 (In)) c) (2 points) What are the constraints of the problem? Clearly explain each constraint in English and provide the mathematical formulation. We have in house capacity of 250 hours for cutting department So, constraint for cutting department 0.4 C1 (In) + 0.8 C2 (In)+ 0.7 C3 (In) +0.3 D1 (In)+ 0.2 D2 (In) = 200 simulaily for C2, C3, D1 and D2 components demand constraint (C2 (in)+ C2 (Out))>= 250 (C3 (in)+ c3 (Out))>= 150 (D1 (in)+ D1 (Out))>= 45 (D2 (in)+ D2 (Out))>= 50 d) (1 points) Are there any sign or type restrictions in your formulation? Why or why not? Clearly explain the sign and type restrictions (if any). Since production and purchasing of component can not be negative Therefore, C1 (In), C1 (Out), C2 (In), C2 (Out),C3 (In), C3 (Out),D1 (In), D1 (Out), D2 (In), And D2 (Out) >=0 Non-negativity constraints: All the decision variables must be >= 0. Integers constraints: All the decision variables must be integer. e) Prepare a spreadsheet to determine the optimal production plan using Excel Solver. I. (2 points) Provide a screenshot of your spreadsheet model. The screenshot should show all the cells involved in formulating the optimization problem. NOTE: Do not copy and paste your spreadsheet to your answer report as an Excel object. Instead, capture a screenshot in Excel and paste this as an image ii. (2 points) Provide a screenshot of your spreadsheet with the formula view. You can switch from normal view to formula view in Excel by clicking the CTRL and keys on your keyboard simultaneously. ii. (2 points) Prepare the Solver model by logging all the information to the Solver Parameters window in Excel. Provide a screenshot of the Solver Parameters window in Excel. iv. (2 points) Finally, solve the optimization problem using the Simplex LP method in Excel Solver. What is the optimal solution, i.e. the optimal values of the objective function and the decision variables? f) (1 point) Compute the labor utilization at each department B) (2 points) Suppose the company hires new employees and the available labor hours for the fabrication department goes up to 220 hours per month. What effect does this have on the optimal product mix and the optimal cost? What is the change in the optimal cost value? Can you explain clearly why the cost changes (or does not change) when more employees are available at the fabrication department? h) (3 points) Answer this question independent of part g: Suppose the company did not have the capacity limits requirements as stated in Table 05.3. What would be the optimal product mix for the company? Use Excel Solver to find the new solution. What is the new optimal product mix and the new optimal cost? Is the new optimal cost lower or higher than the one in part (e)? Why do you 15 think this is? Explain clearly. Is having contracts with clients and committing to deliveries to clients beneficial in this problem? Explain clearly why or why not. Question 5. (22 points) OPTIMAL PRODUCT MIX AND WHAT-IF QUESTIONS AU Electronics manufactures is the supplier of components C1, C2 and C3 for the production of screens and components D1 and D2 for the production of frames for KTVs. Screens and frames are produced by other manufacturers. Demand for the components has increased recently and meeting this demand will test the company's production capacities. Any of the components C1, C2, C3, D1 and D2 may need to be purchased by AU Electronics from outside suppliers because there is limited in-house capacity. The variable in-house production cost per unit is compared with the outside purchase cost in the following table. Component Outside Variable Inside Production Cost (per unit) Cost (per unit) C1 1.21 0.81 C2 2.50 2.30 C3 1.95 1.45 D1 0.74 0.42 D2 1.10 0.70 Table-Q5.1. Variable in-house and outside cost of the components AU Electronics Company's plant consists of three departments. The labor requirements in hours of each component in each department if manufactured in-house are summarized in the following table. The labor hours available for a motor production are listed in the last row. Availability of labor limits the in-house production capacity for the components. However, there is unlimited supply if the company decides to purchase the components from outside vendors. Component Cutting Department (hours per unit) 0.4 0.8 Shaping Department (hours per unit) 0.6 0.2 0.9 C1 C2 Fabrication Department (hours per unit) 0.4 0.5 0.6 c3 0.7 D1 0.3 0.3 0.1 D2 0.2 0.4 0.2 Capacity (total available labor hours) 250 325 175 Table-25.2. Labor hour requirements per unit produced and monthly available labor hours at each department The company is already in a contract with clients for the next month. The confirmed number of components to be delivered are given in Table-05-3. These numbers show the number of components the company has committed to sell and is the minimum demand AU Electronics must meet. Component C1 C2 C3 D1 D2 Minimum number of products to be sent to clients next month 200 250 150 45 50 Table-25.3. Confirmed demand for next month You are asked to determine the optimal product mix (i.e., the monthly number of each product type to be provided) that minimizes AU Electronics' production total production and purchasing costs for next month. You will formulate a linear programming model to determine the optimal solution using Excel Solver 1 NOTE: SHOW ALL YOUR WORK. a) (3 points) What are the decision variables? How many decision variables are there? Clearly explain the decision variables in English and provide the mathematical notation used in the algebraic formulation of the decision problem. Decision variables: Let C1(In)- number of C1 component produced in house C1 (out)- number of Ci component purchasing from outside C2 (In)- number of C2 component produced in house C2 (out)- number of C2 component purchasing from outside C3 (In)- number of C3 component produced in house C3 (out)- number of C3 component purchasing from outside D1 (In)- number of D1 component produced in house D1 (out)- number of D1 component purchasing from outside D2 (In)- number of D2 component produced in house D2 (out)- number of D2 component purchasing from outside There are 10 decision variables. b) (2 points) What is the objective function? Clearly explain the objective function in English and provide the mathematical formulation. To minimise the cost of production in house and purchasing from outside as well. So, objective function Z= Min(1.21 C1(out) +0.81 C1 (In) + 2.5 C2 (out)+ 2.30 C2 (In)+ 1.95 C3(Out) + 1.45 C3(In) + 0.74 D1(out) +0.42 D1 (In)+1.10 D2(out)+ 0.7 D2 (In)) c) (2 points) What are the constraints of the problem? Clearly explain each constraint in English and provide the mathematical formulation. We have in house capacity of 250 hours for cutting department So, constraint for cutting department 0.4 C1 (In) + 0.8 C2 (In)+ 0.7 C3 (In) +0.3 D1 (In)+ 0.2 D2 (In) = 200 simulaily for C2, C3, D1 and D2 components demand constraint (C2 (in)+ C2 (Out))>= 250 (C3 (in)+ c3 (Out))>= 150 (D1 (in)+ D1 (Out))>= 45 (D2 (in)+ D2 (Out))>= 50 d) (1 points) Are there any sign or type restrictions in your formulation? Why or why not? Clearly explain the sign and type restrictions (if any). Since production and purchasing of component can not be negative Therefore, C1 (In), C1 (Out), C2 (In), C2 (Out),C3 (In), C3 (Out),D1 (In), D1 (Out), D2 (In), And D2 (Out) >=0 Non-negativity constraints: All the decision variables must be >= 0. Integers constraints: All the decision variables must be integer. e) Prepare a spreadsheet to determine the optimal production plan using Excel Solver. I. (2 points) Provide a screenshot of your spreadsheet model. The screenshot should show all the cells involved in formulating the optimization problem. NOTE: Do not copy and paste your spreadsheet to your answer report as an Excel object. Instead, capture a screenshot in Excel and paste this as an image ii. (2 points) Provide a screenshot of your spreadsheet with the formula view. You can switch from normal view to formula view in Excel by clicking the CTRL and keys on your keyboard simultaneously. ii. (2 points) Prepare the Solver model by logging all the information to the Solver Parameters window in Excel. Provide a screenshot of the Solver Parameters window in Excel. iv. (2 points) Finally, solve the optimization problem using the Simplex LP method in Excel Solver. What is the optimal solution, i.e. the optimal values of the objective function and the decision variables? f) (1 point) Compute the labor utilization at each department B) (2 points) Suppose the company hires new employees and the available labor hours for the fabrication department goes up to 220 hours per month. What effect does this have on the optimal product mix and the optimal cost? What is the change in the optimal cost value? Can you explain clearly why the cost changes (or does not change) when more employees are available at the fabrication department? h) (3 points) Answer this question independent of part g: Suppose the company did not have the capacity limits requirements as stated in Table 05.3. What would be the optimal product mix for the company? Use Excel Solver to find the new solution. What is the new optimal product mix and the new optimal cost? Is the new optimal cost lower or higher than the one in part (e)? Why do you 15 think this is? Explain clearly. Is having contracts with clients and committing to deliveries to clients beneficial in this problem? Explain clearly why or why not