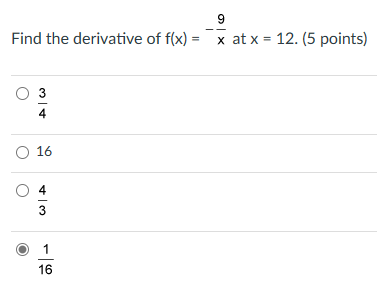
Please answer the questions

#1

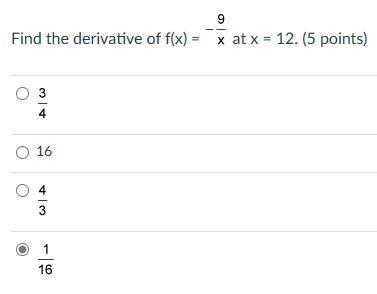
4. Find all polar coordinates of point P where P = . (5 points) O (4, 3 + 2nn) or (-4, 3 + (2n + 1)) O (4, 3 + (2n + 1)nt) or (-4, 3 + 2nn) O (4, 3 + 2nnt) or (4, 3 + (2n + 1)n) O A (4. 3 + 2nn) or (-4, 3 + 2nn)\fFind the exact value by using a half-angle identity. (5 points) sin 12 2 O V2 - V3 O V2+ 13 O V2- V3\fFind the exact values of the indicated trigonometric functions. Write fractions in lowest terms. C 96 B 28 100 A Find sin B and tan B. (5 points) O 7 sin B = 24 ; tan B = 25 O 24 24 sin B = 25 ; tan B = 7 O 7 7 sin B = 25 ; tan B = 24 O 25 24 sin B = 7 ; tan B = 7Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the polynomial in standard form. 5, -3, and -1 + 2i (5 points) Of(x) = x4 - 4x3 + 10x2 + 20x +75 O f(x) = x4 - 14x2 - 40x - 75 Of(x) = x4 - 4x3- 10x2 - 20x - 75 Of(x) = x4+ 10x2 - 40x - 75Using the given zero, find all other zeros of f(x). -2i is a zero of f(x) = x4 - 5x2 - 36 (5 points) O 2i, 6i, -6i 2i, 3i, -3i 2i, 6, -6 O 2i, 3, -3