Question: Please answer these questions clearly with a box around the answer. fThe dilferential operator D2 7 121) + 37 has the form D2 7 20D
Please answer these questions clearly with a box around the answer.


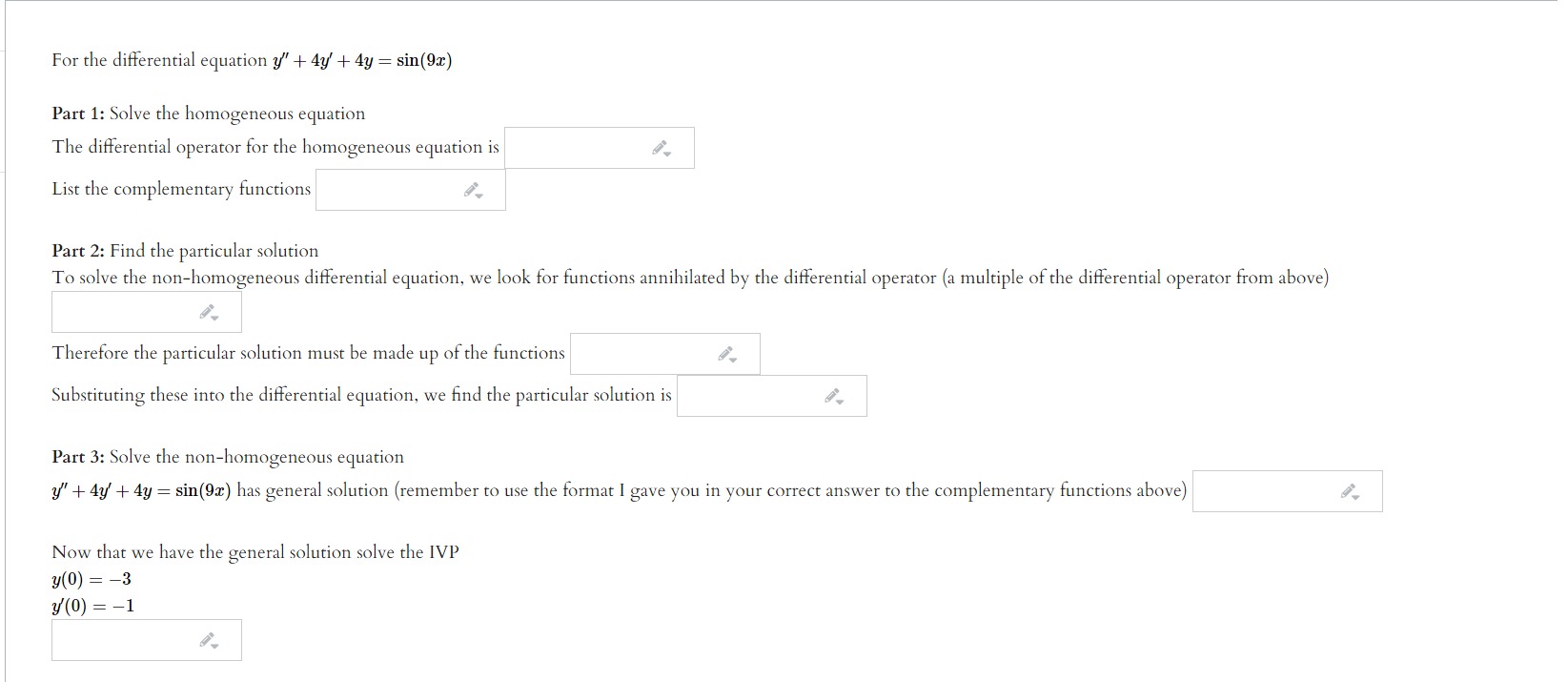
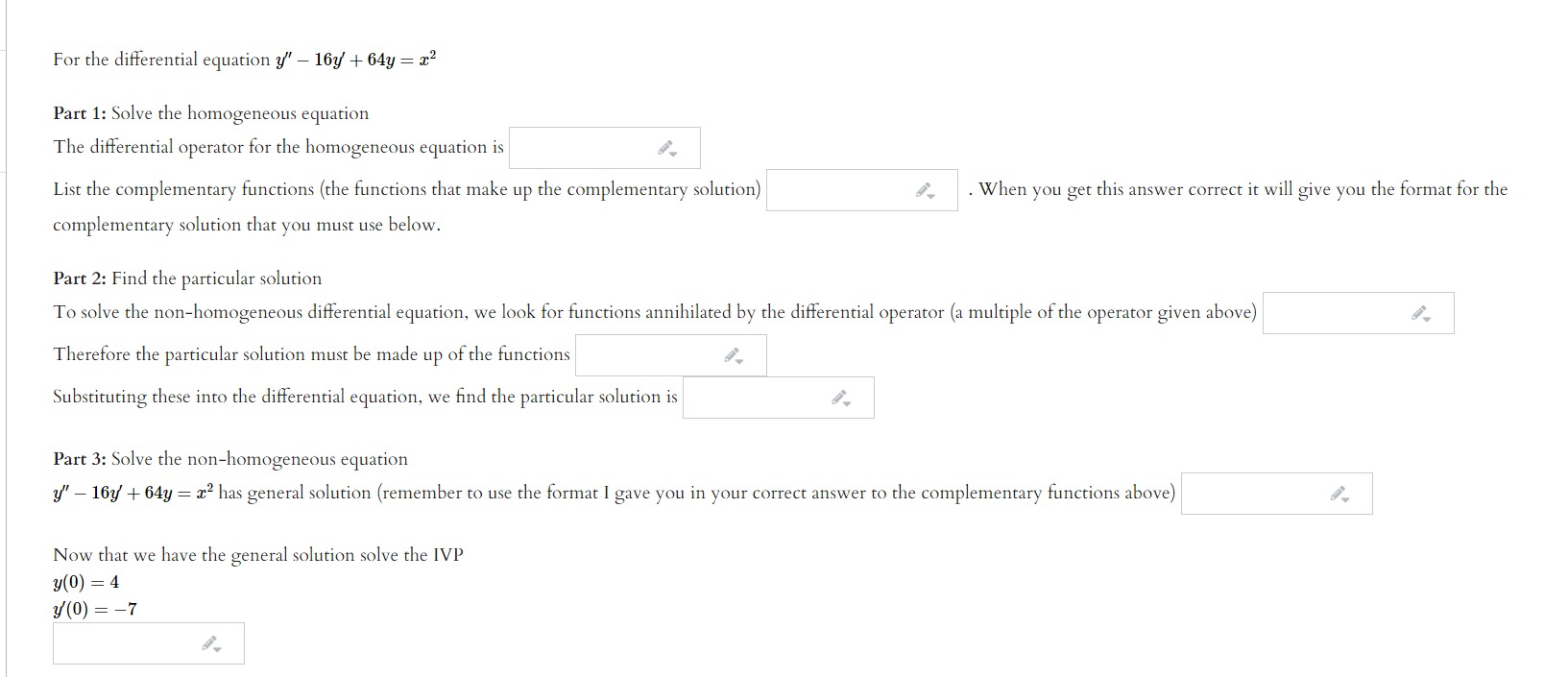

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


