Please answer this question for me and provide as much detail as you can. I would like to understand the concepts and follow along. Thank you so much!!

I have also provided the Equation 14.2 required to solve the problem in the second image.

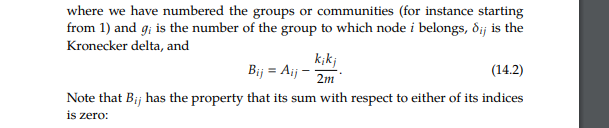
an algorithm that can fina all the bicomponents in a network. 8.3 Suppose you have a sparse undirected network with m complexity of n. What is the time a) Multiplying an arbitrary n-element vector by the adjacency matrix, if the network is stored in adjacency matrix format. b) The same multiplication if the network is in adjacency list format. c) The "modularity matrix" B of an undirected network is the nxn symmetric matrix with elements kjk (See Eq. (14.2) on page 500.) What is the time complexity for multiplying an arbitrary vector by the modularity matrix of our sparse network if the network is in adjacency list format? Describe briefly an algorithm that achieves this. (Hint: One's first guess might be that the multiplication takes time O(n2) but it is possible to do it faster than this in the sparse network case.) where we have numbered the groups or communities (for instance starting Kronecker delta, and k;k (14.2) Note that Bij has the property that its sum with respect to either of its indices is zero: an algorithm that can fina all the bicomponents in a network. 8.3 Suppose you have a sparse undirected network with m complexity of n. What is the time a) Multiplying an arbitrary n-element vector by the adjacency matrix, if the network is stored in adjacency matrix format. b) The same multiplication if the network is in adjacency list format. c) The "modularity matrix" B of an undirected network is the nxn symmetric matrix with elements kjk (See Eq. (14.2) on page 500.) What is the time complexity for multiplying an arbitrary vector by the modularity matrix of our sparse network if the network is in adjacency list format? Describe briefly an algorithm that achieves this. (Hint: One's first guess might be that the multiplication takes time O(n2) but it is possible to do it faster than this in the sparse network case.) where we have numbered the groups or communities (for instance starting Kronecker delta, and k;k (14.2) Note that Bij has the property that its sum with respect to either of its indices is zero