please answer using data

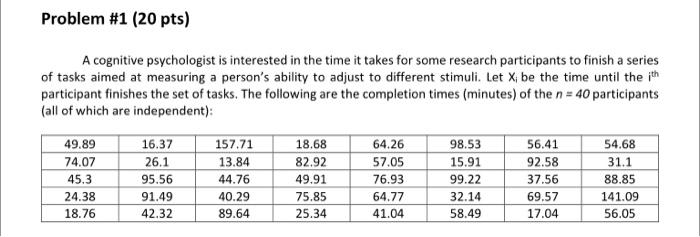
49.89, 16.37, 157.71, 18.68, 64.26, 98.53, 56.41, 54.68,

74.07, 26.1, 13.84, 82.92, 57.05, 15.91, 92.58, 31.1,

45.3, 95.56, 44.76, 49.91, 76.93, 99.22, 37.56, 88.85,

24.38, 91.49, 40.29, 75.85, 64.77, 32.14, 69.57, 141.09,

18.76, 42.32, 89.64, 25.34, 41.04, 58.49, 17.04, 56.05

please answer parts e-g (I put a text file of the data as well)

Problem #1 (20 pts) A cognitive psychologist is interested in the time it takes for some research participants to finish a series of tasks aimed at measuring a person's ability to adjust to different stimuli. Let X be the time until the ith participant finishes the set of tasks. The following are the completion times (minutes) of the n = 40 participants (all of which are independent): 49.89 74.07 45.3 24.38 18.76 16.37 26.1 95.56 91.49 42.32 157.71 13.84 44.76 40.29 89.64 18.68 82.92 49.91 75.85 25.34 64.26 57.05 76.93 64.77 41.04 98.53 15.91 99.22 32.14 58.49 56.41 92.58 37.56 69.57 17.04 54.68 31.1 88.85 141.09 56.05 c.) (2 pts) What are the Method of Moment and Maximum Likelihood estimates for B? )(5 pts) It turns out that Gamma 21.2) Using this information and the data above to construct a 95% confidence interval for E[X] (ie. for the quantity you found in b.). (Hint: Be careful when using R. for gommao,b) you must use the reciprocal of b, eg. "X"gammal a = 2,6 = 1/6). where x is either n". *. pora"). 8.) (Bonus 3pts.) What is something special about the distribution in e.)? Can you make an adjustment to your confidence interval to include this something special? A cognitive psychologist is interested in the time it takes for some research participants to finish a series of tasks aimed at measuring a person's ability to adjust to different stimuli. Let Xibe the time until the ith participant finishes the set of tasks. The following are the completion times (minutes) of the n = 40 participants (all of which are independent): 49.89 74.07 45.3 24.38 18.76 16.37 26.1 95.56 91.49 42.32 157.71 13.84 44.76 40.29 89.64 18.68 82.92 49.91 75.85 25.34 64.26 57.05 76.93 64.77 41.04 98.53 15.91 99.22 32.14 58.49 56.41 92.58 37.56 69.57 17.04 54.68 31.1 88.85 141.09 56.05 (Please see the attached txt file for this raw data) The cognitive psychologist has reason to believe that the population distribution for the time to complete these tasks is as follows: otherwise f) (5 pts) it turns out that 2X B Gamma(2n, 2) Using this information and the data above to construct a 95% confidence interval for E[X] (i.e. for the quantity you found in b.). (Hint: Be careful when using R, for gamma(a,b) you must use the reciprocal of b, e.g. "x"gammal, a = a, 6 = 1/b), where x is either "n", "d", "p", or "q"). e.) (2 pts) What are the Method of Moment and Maximum Likelihood estimates for B? 8.) (Bonus 3pts.) What is something special about the distribution in e.)? Can you make an adjustment to your confidence interval to include this something special? Problem #1 (20 pts) A cognitive psychologist is interested in the time it takes for some research participants to finish a series of tasks aimed at measuring a person's ability to adjust to different stimuli. Let X be the time until the ith participant finishes the set of tasks. The following are the completion times (minutes) of the n = 40 participants (all of which are independent): 49.89 74.07 45.3 24.38 18.76 16.37 26.1 95.56 91.49 42.32 157.71 13.84 44.76 40.29 89.64 18.68 82.92 49.91 75.85 25.34 64.26 57.05 76.93 64.77 41.04 98.53 15.91 99.22 32.14 58.49 56.41 92.58 37.56 69.57 17.04 54.68 31.1 88.85 141.09 56.05 c.) (2 pts) What are the Method of Moment and Maximum Likelihood estimates for B? )(5 pts) It turns out that Gamma 21.2) Using this information and the data above to construct a 95% confidence interval for E[X] (ie. for the quantity you found in b.). (Hint: Be careful when using R. for gommao,b) you must use the reciprocal of b, eg. "X"gammal a = 2,6 = 1/6). where x is either n". *. pora"). 8.) (Bonus 3pts.) What is something special about the distribution in e.)? Can you make an adjustment to your confidence interval to include this something special? A cognitive psychologist is interested in the time it takes for some research participants to finish a series of tasks aimed at measuring a person's ability to adjust to different stimuli. Let Xibe the time until the ith participant finishes the set of tasks. The following are the completion times (minutes) of the n = 40 participants (all of which are independent): 49.89 74.07 45.3 24.38 18.76 16.37 26.1 95.56 91.49 42.32 157.71 13.84 44.76 40.29 89.64 18.68 82.92 49.91 75.85 25.34 64.26 57.05 76.93 64.77 41.04 98.53 15.91 99.22 32.14 58.49 56.41 92.58 37.56 69.57 17.04 54.68 31.1 88.85 141.09 56.05 (Please see the attached txt file for this raw data) The cognitive psychologist has reason to believe that the population distribution for the time to complete these tasks is as follows: otherwise f) (5 pts) it turns out that 2X B Gamma(2n, 2) Using this information and the data above to construct a 95% confidence interval for E[X] (i.e. for the quantity you found in b.). (Hint: Be careful when using R, for gamma(a,b) you must use the reciprocal of b, e.g. "x"gammal, a = a, 6 = 1/b), where x is either "n", "d", "p", or "q"). e.) (2 pts) What are the Method of Moment and Maximum Likelihood estimates for B? 8.) (Bonus 3pts.) What is something special about the distribution in e.)? Can you make an adjustment to your confidence interval to include this something special