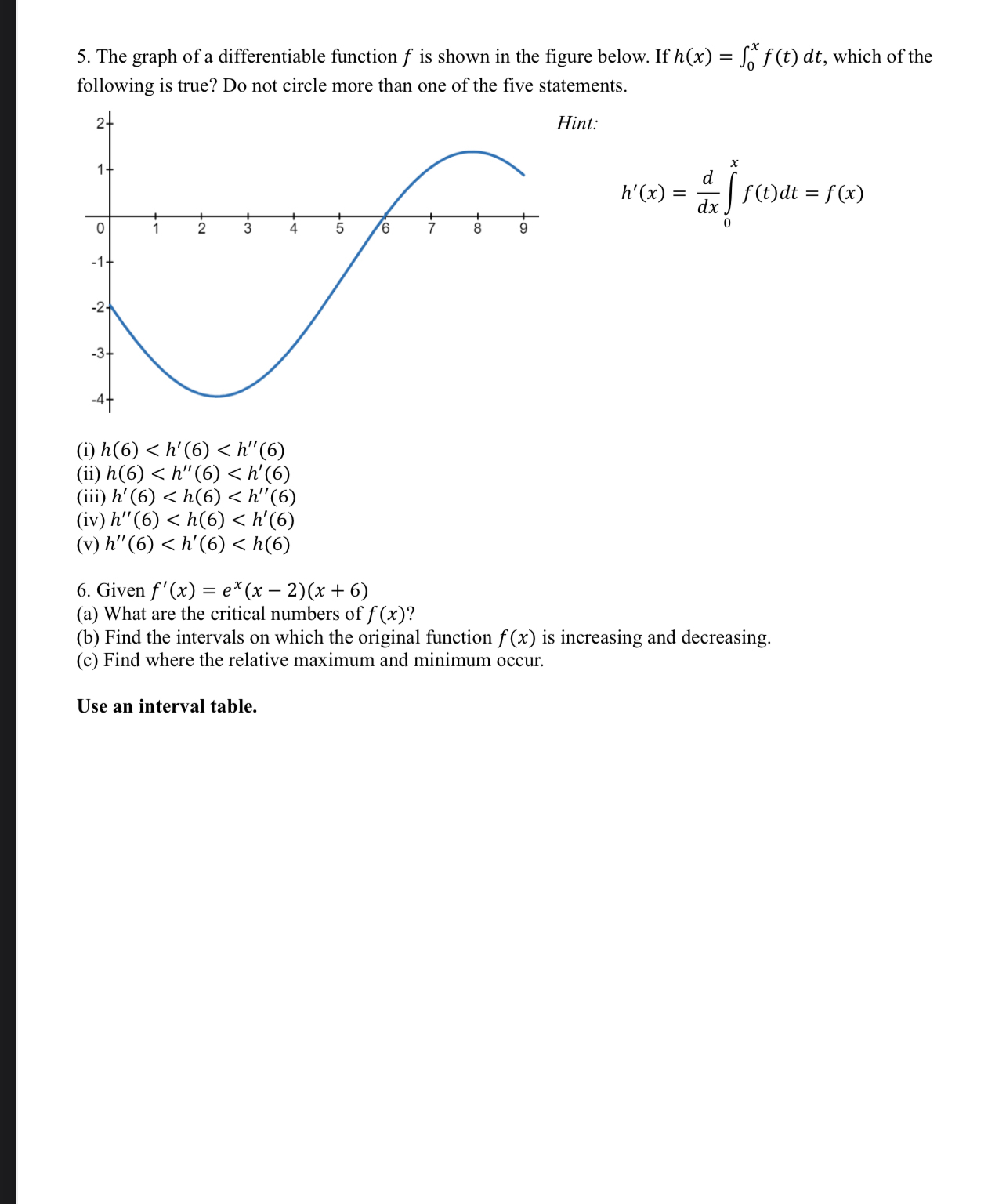
PLEASE ANSWER WITH COMPLETE SOLUTION AND ALL THE SUB QUESTIONS BELOW

The graph of a differentiable function $f$ is shown in the figure below. If $h(x)={\displaystyle \underset{0}{\overset{x}{}}}f(t)dt,$ which of the following is true? Do not circle more than one of the five statements.

Fint:

$h^{\text{'}}(x)=\frac{d}{dx}{\displaystyle \underset{0}{\overset{x}{}}}f(t)dt=f(x)$

$($i$)f^{\text{'}}(x)=e^x(x-2)(x+6)f(x)f(x)h^{\text{'}\text{'}}(6)$

$6.$ Given $f^{\text{'}}(x)=e^x(x-2)(x+6)$

$(a)$ What are the critical numbers $off(x)?$

$(b)$ Find the intervals $on$ which the original function $f(x)is$ increasing and decreasing.

$(c)$ Find where the relative maximum and minimum occur.

Use $an$ interval table.$h^{\text{'}\text{'}}(6)$

$(v)h^{\text{'}\text{'}}(6)$

$6.$ Given $f^{\text{'}}(x)=e^x(x-2)(x+6)$

$(a)$ What are the critical numbers $off(x)?$

$(b)$ Find the intervals $on$ which the original function $f(x)is$ increasing and decreasing.

$(c)$ Find where the relative maximum and minimum occur.

Use $an$ interval table.$h^{\text{'}}(6)$

$(iv)h^{\text{'}\text{'}}(6)$

$(v)h^{\text{'}\text{'}}(6)$

$6.$ Given $f^{\text{'}}(x)=e^x(x-2)(x+6)$

$(a)$ What are the critical numbers $off(x)?$

$(b)$ Find the intervals $on$ which the original function $f(x)is$ increasing and decreasing.

$(c)$ Find where the relative maximum and minimum occur.

Use $an$ interval table.$h(6)$

$(iii)h^{\text{'}}(6)$

$(iv)h^{\text{'}\text{'}}(6)$

$(v)h^{\text{'}\text{'}}(6)$

$6.$ Given $f^{\text{'}}(x)=e^x(x-2)(x+6)$

$(a)$ What are the critical numbers $off(x)?$

$(b)$ Find the intervals $on$ which the original function $f(x)is$ increasing and decreasing.

$(c)$ Find where the relative maximum and minimum occur.

Use $an$ interval table.$h(6)$

$(ii)h(6)$

$(iii)h^{\text{'}}(6)$

$(iv)h^{\text{'}\text{'}}(6)$

$(v)h^{\text{'}\text{'}}(6)$

$6.$ Given $f^{\text{'}}(x)=e^x(x-2)(x+6)$

$(a)$ What are the critical numbers $off(x)?$

$(b)$ Find the intervals $on$ which the original function $f(x)is$ increasing and decreasing.

$(c)$ Find where the relative maximum and minimum occur.

Use $an$ interval table.