please check the template

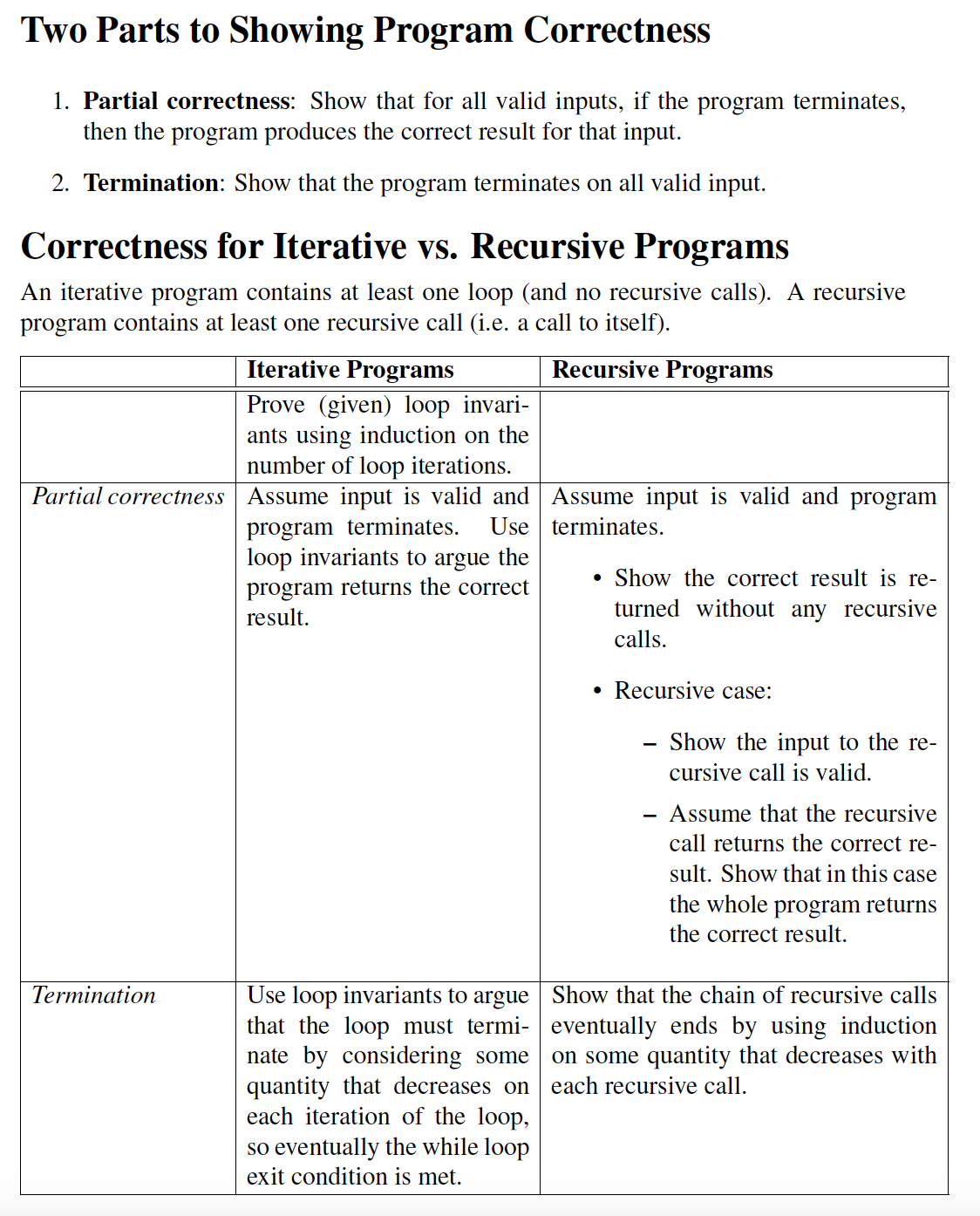
Two Parts to Showing Program Correctness 1. Partial correctness: Show that for all valid inputs, if the program terminates, then the program produces the correct result for that input. 2. Termination: Show that the program terminates on all valid input. Correctness for Iterative vs. Recursive Programs An iterative program contains at least one loop (and no recursive calls). A recursive program contains at least one recursive call (i.e. a call to itself). Iterative Programs Recursive Programs Prove (given) loop invari- ants using induction on the number of loop iterations. Partial correctness Assume input is valid and program terminates. Use loop invariants to argue the program returns the correct result. Assume input is valid and program terminates. - Show the correct result is re turned without any recursive calls. - Recursive case: Show the input to the re cursive call is valid. Assume that the recursive call returns the correct re sult. Show that in this case the whole program returns the correct result. Termination Use loop invariants to argue that the loop must tenni- nate by considering some quantity that decreases on each iteration of the loop, so eventually the while loop exit condition is met. Show that the chain of recursive calls eventually ends by using induction on some quantity that decreases with each recursive call. 4. Consider the following program specification and implementation for determin- ing the mth Fibonacci number fm for m E N. (Recall that the Fibonacci sequence is defined as fo = 0, f1 = 1, and fm = fm-1 + fm-2 for m > 2.) rec fib(m) for me N (1) if m = 0 return 0 (2) else if m = 1 return 1 (3) else return rec fib(m - 1) + rec_fib(m -2) {output is fm, where fm is the mth Fibonacci number} N CS-MATH 240: Spring 2021 (a) Trace the execution of rec fib(m) for the calls m = 1 up to m = 5. It may help to draw this as a branching tree, as on page 387 on Rosen (at the beginning of subsection 5.4.3). (b) Prove the correctness of rec_fib by arguing (i) partial correctness and (ii) termination