Please choose the appropriate(s) equation(s) to solve the problem

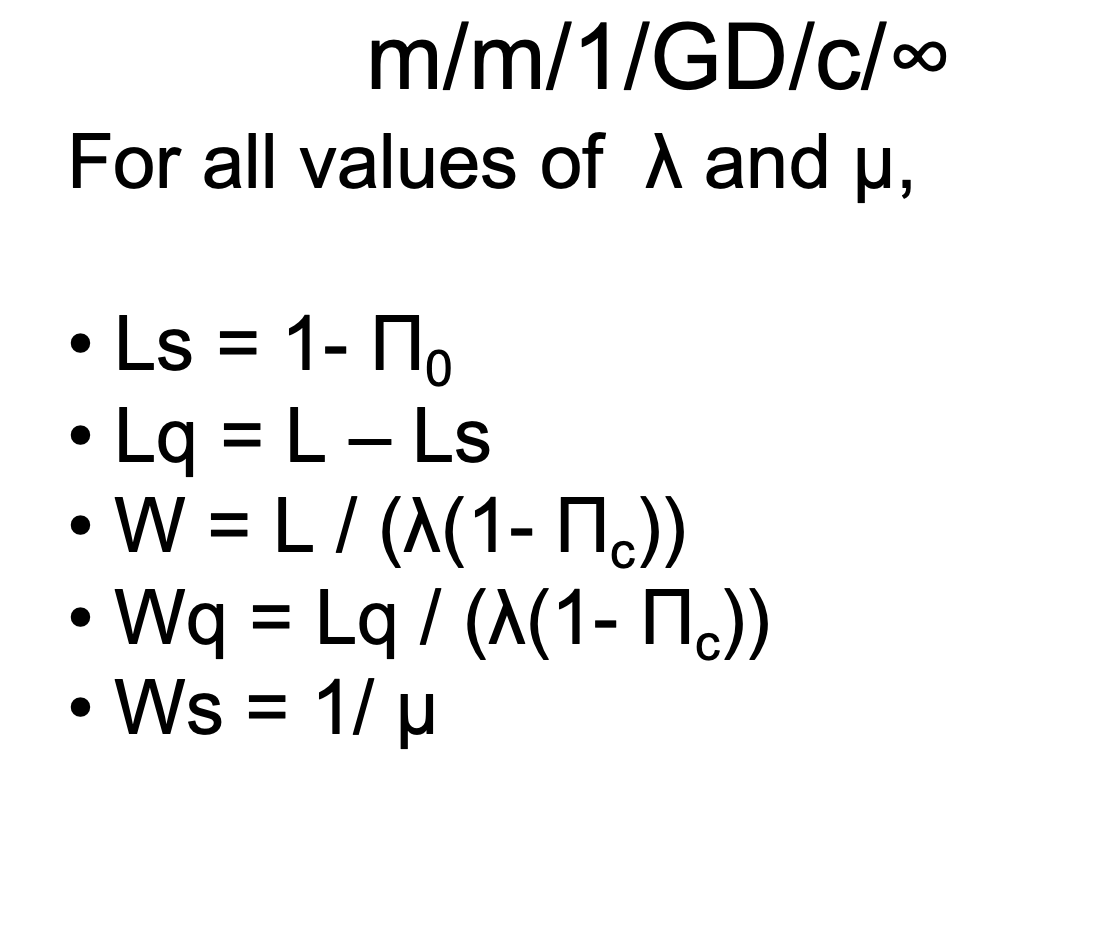
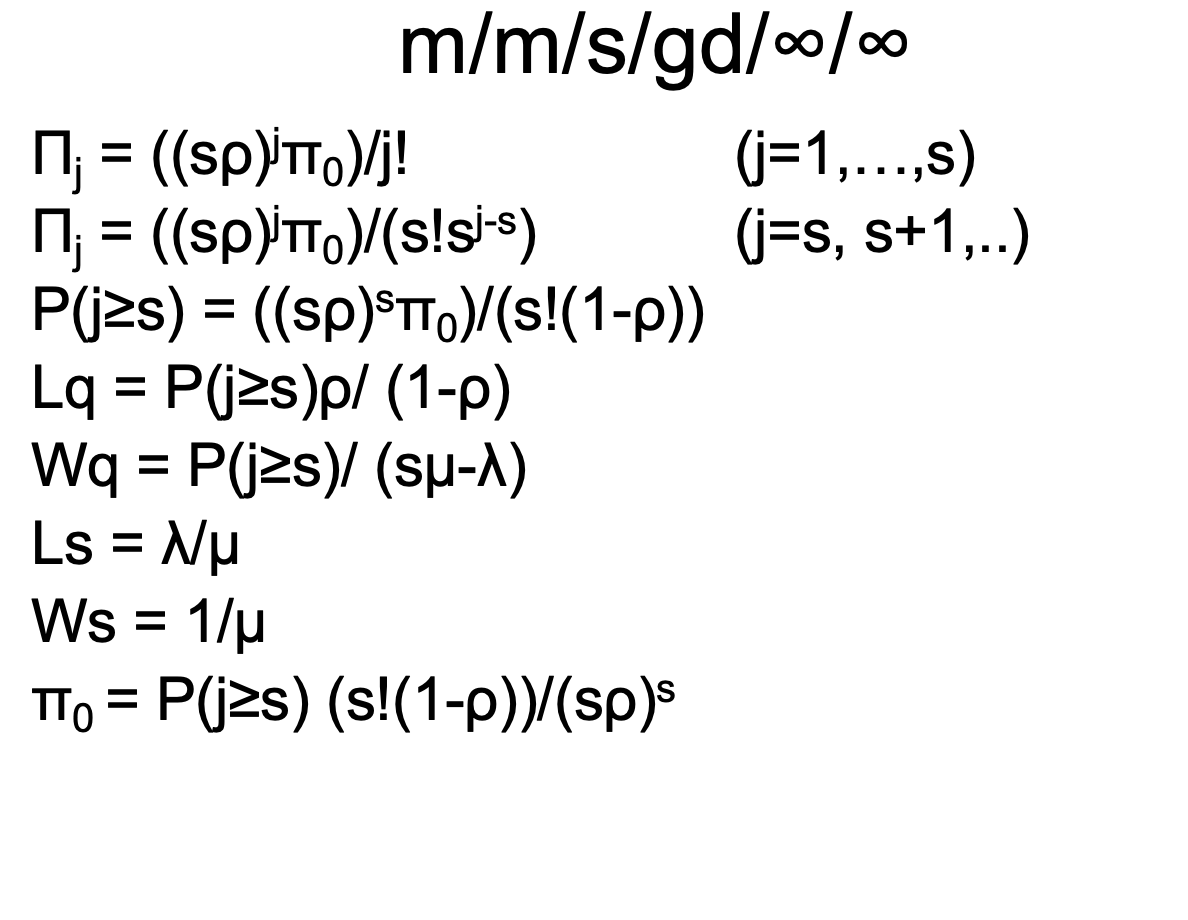
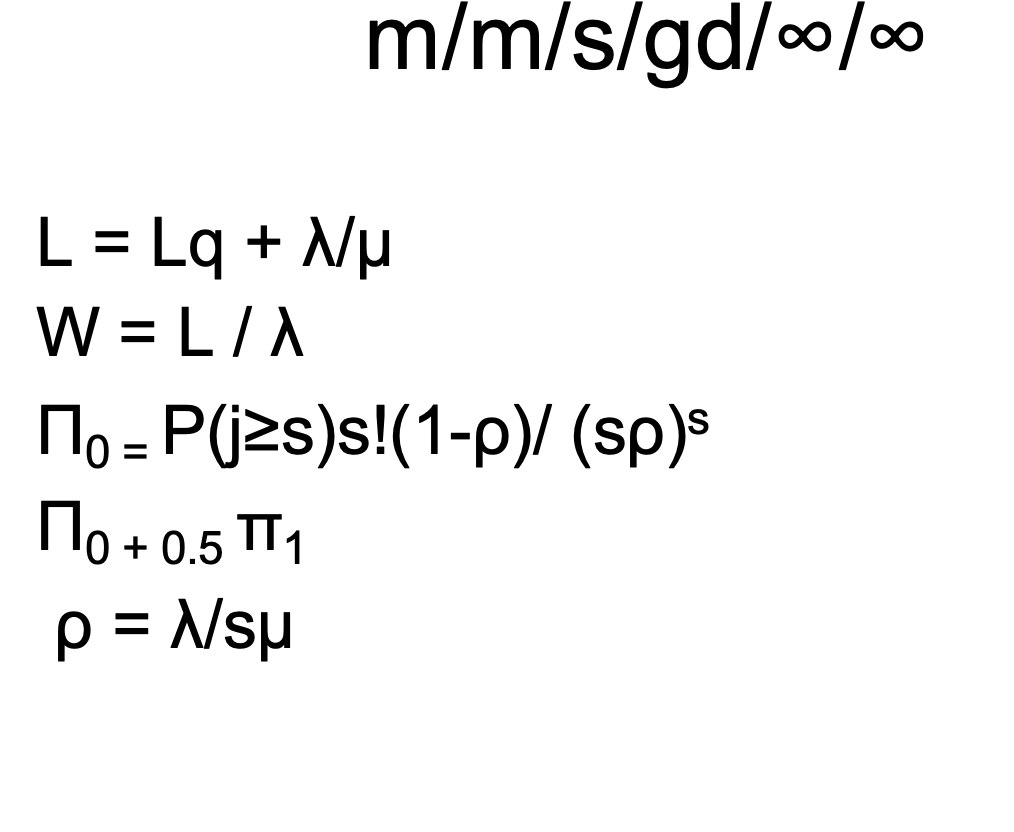
A hair salon does not make appointments, but runs the salon on a first come, first served basis. She finds that she is extremely busy on Saturday mornings,

so she is considering hiring a part time assistant. Customers seem to arrive according to a Poison process with a mean arrival rate of 4 per hour. Customers

are willing to wait for a haircut. From data, the customer processing time is exponentially distributed with an average of 15 minutes. The minimum hair

dressers are to supply the demand is?

a.s=6

b.s = 13

c. S = 4

d.s=2

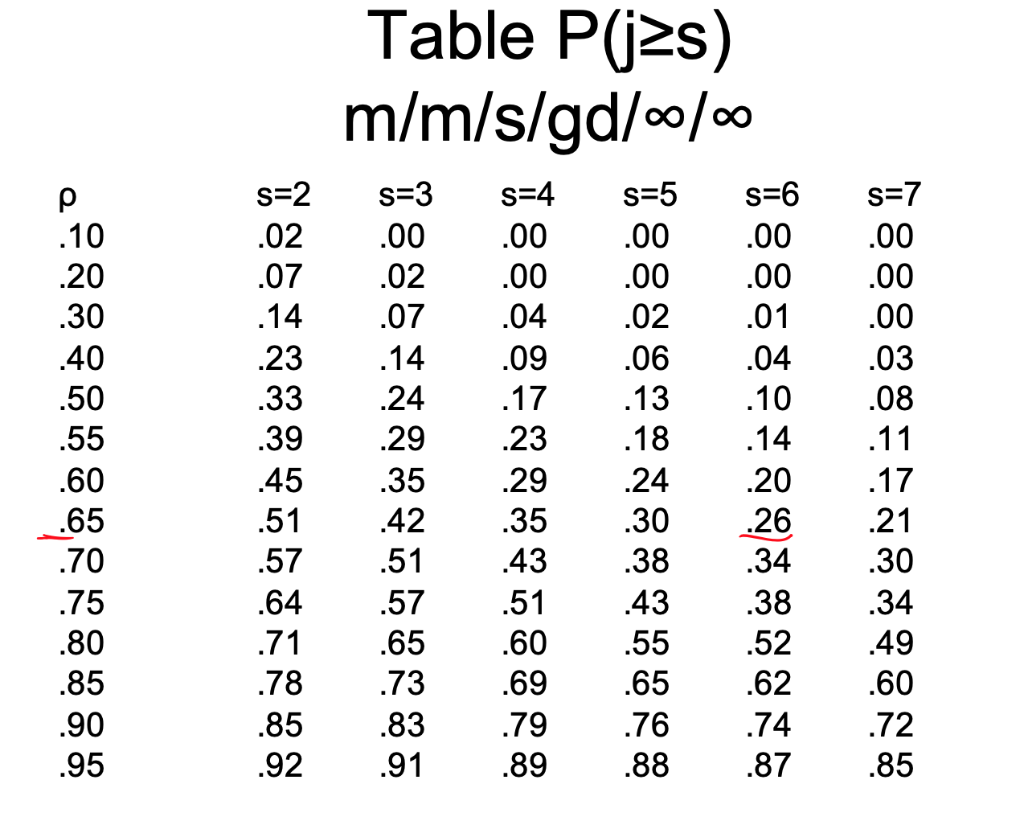
1 = average number of arrivals entering the system per unit of time. L = average number of customers present in the queuing system Lq = average number of customers waiting in line. Ls = average number of customers in service. = W = average time a customer spends in the system. Wq = average time a customer spends in the line. Ws = average time a customer spends in service. Mj = probability of j customers in the system. - M/M/1/GD//o Queuing System p = N/su s =1 = 1- L=p/(1-P) W = L/X = p / (^(1 - 0)) = 1/(u -) A2) Lq = A2 1 (u(A)) W = L/\ = N(U(u )) 0 = . = = . = . = Ls = p 1/ . Ws = 1/ u Equations m/m/1/GD/c/ If Eu, 10 = (1-P)/(1-pc+1) n = pin. (j = 1,2, ..., c) L = p[1 (c+1) pc + c pc+1] / ((1- pc+1) 1 - )) = + - If I = u, m;= 1/(c+1) (j = 0,1,2...,c) L = c/2 = = m/m/1/GD/c/ For all values of land u, = Ls = - 1- Lq = L-LS W = L1 (1(1-1) Wq = Lq/((1-1)) Ws = 1/ u . . Equations m/m/s/gd// Inter arrival and service times are exponential. Assume a single line with multiple with several servers. Whenever j customers are present, min (j, s) server will be occupied, thus Mj = min (j, s)*u. 1; = 1 (j = 0,1,...) Hj = ju (j =0,1, ... s) Mj = su (J = 5+1, s+2,...) = = = m/m/s/gd/olo ; = ((sp)'Tto)/j! = (j=1,...,s) 0} = ((sp)'To)/(s!Si-s) N (j=s, s+1,..) P(js) = ((sp)STT.)/(s!(1-2)) Lq = P(js)p/ (1-0) Wq = P(js)/ (su-x) Ls = Nu Ws = 1/4 TTo = P(js) (s!(1-0))/(sp)s = = m/m/s/gd/|o L = Lq + Nu W = LI 1.- P(js)s!(1-p(sp) Mo + 0.5 T1 p = Nsu 0 = = Table P(j=s) m/m/s/gd/o/o p .10 .20 .30 .40 .50 .55 .60 .65 .70 .75 .80 .85 .90 .95 s=2 .02 .07 .14 .23 .33 .39 .45 .51 .57 .64 .71 .78 .85 .92 s=3 .00 .02 .07 .14 .24 .29 .35 .42 .51 .57 .65 .73 .83 .91 s=4 .00 .00 .04 .09 .17 .23 .29 .35 .43 .51 .60 .69 .79 .89 s=5 .00 .00 .02 .06 .13 .18 .24 .30 .38 43 .55 .65 .76 .88 s=6 .00 .00 .01 .04 .10 .14 .20 .26 .34 .38 .52 .62 .74 s=7 .00 .00 .00 .03 .08 .11 .17 .21 .30 .34 .49 .60 .72 .85 .87