Please choose the appropriate(s) equation(s) to solve the problem

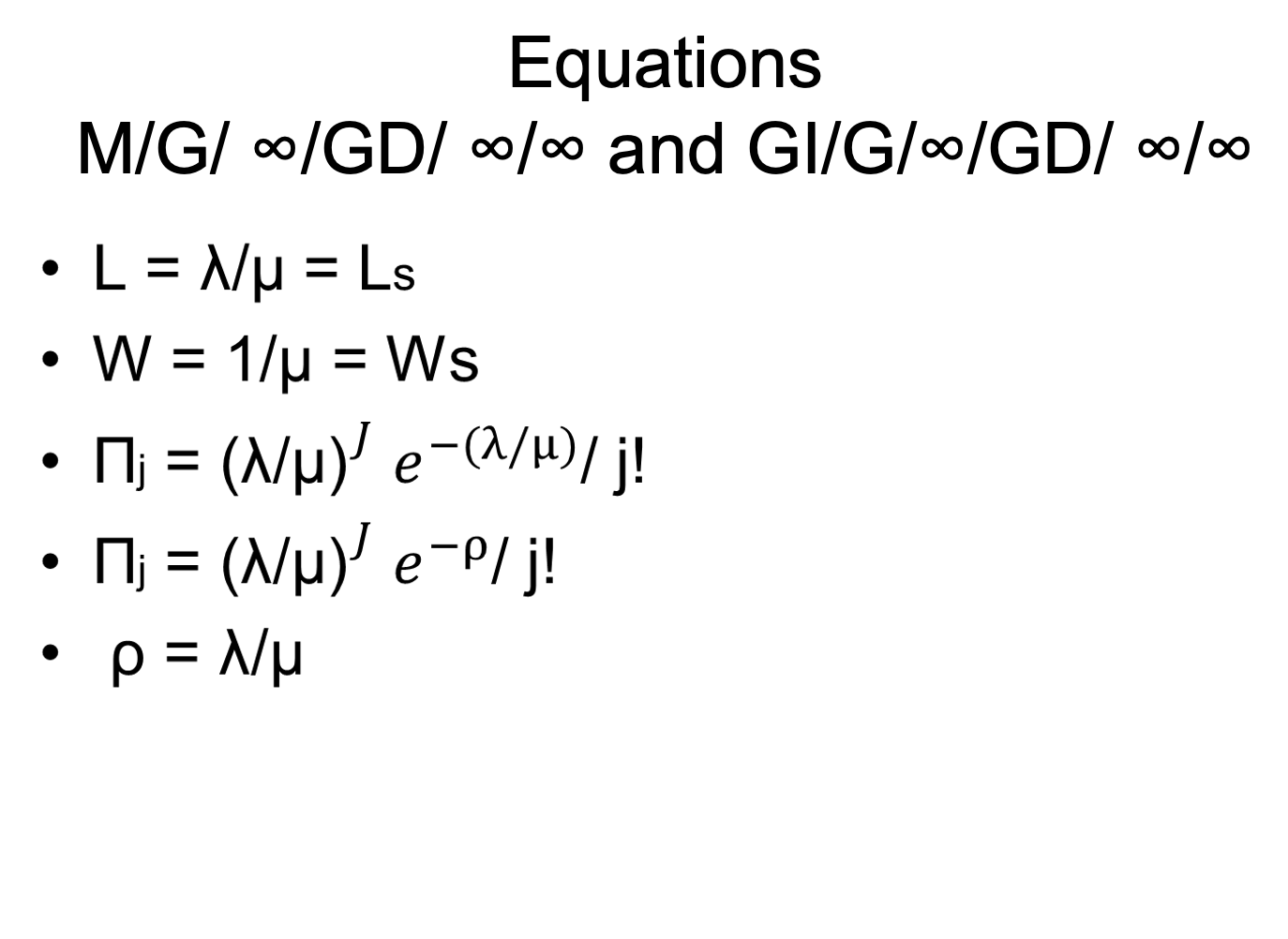
Past record indicate that each laser computer printer needs repair after about 24 hours of use. Breakdowns have been determined to be Poison distributed.

The one technician on duty can service a printer in an average of 2 hour, following an exponential distribution. Assume infinite population. On average, how

many printers will be waiting in line?

a. 12 printers

b. explotes

c. 1 printer

d. 0 printer

1 = average number of arrivals entering the system per unit of time. L = average number of customers present in the queuing system Lq = average number of customers waiting in line. Ls = average number of customers in service. = W = average time a customer spends in the system. Wq = average time a customer spends in the line. Ws = average time a customer spends in service. Mj = probability of j customers in the system. M/G/ -0/GD00/00 and GI/G/0/GD/ 00/00 Infinite servers where a server is available for each arrival Inter arrival times are any common distribution E(A) = 1/ 1 where is the arrival rate. When a customer arrives, immediately enters service. E(S) = 1/4 = = Equations M/G/ 0/GDI 00/00 and GI/G/0/GD/ 00/00 = L = Nu = Ls W = 1/u = Ws 1} = (Nu) e-(W/H)/j! ; = (N) e-P/j! = e O e =