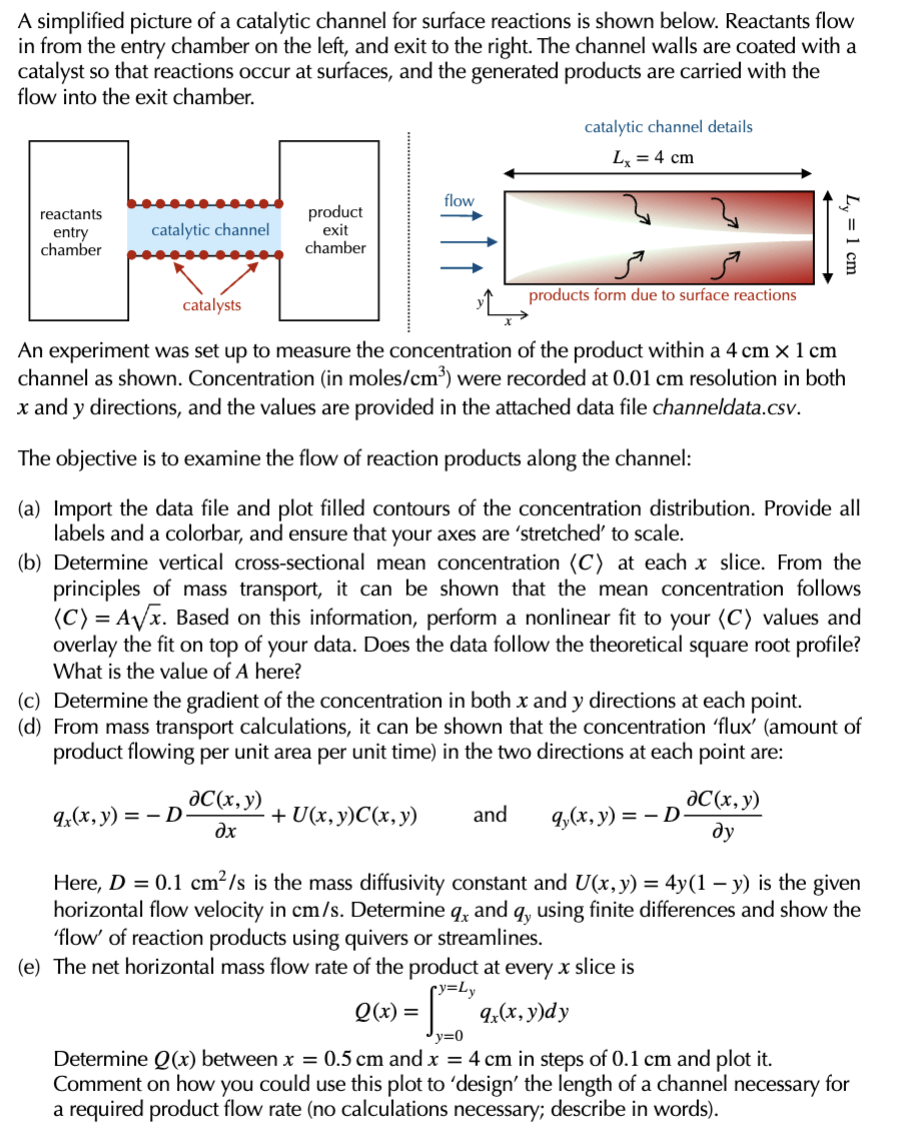
Question: please code in python please A simplified picture of a catalytic channel for surface reactions is shown below. Reactants flow in from the entry chamber
 please code in python please
please code in python please
A simplified picture of a catalytic channel for surface reactions is shown below. Reactants flow in from the entry chamber on the left, and exit to the right. The channel walls are coated with a catalyst so that reactions occur at surfaces, and the generated products are carried with the flow into the exit chamber. An experiment was set up to measure the concentration of the product within a 4cm1cm channel as shown. Concentration (in moles /cm3 ) were recorded at 0.01cm resolution in both x and y directions, and the values are provided in the attached data file channeldata.cSv. The objective is to examine the flow of reaction products along the channel: (a) Import the data file and plot filled contours of the concentration distribution. Provide all labels and a colorbar, and ensure that your axes are 'stretched' to scale. (b) Determine vertical cross-sectional mean concentration C at each x slice. From the principles of mass transport, it can be shown that the mean concentration follows C=Ax. Based on this information, perform a nonlinear fit to your C values and overlay the fit on top of your data. Does the data follow the theoretical square root profile? What is the value of A here? (c) Determine the gradient of the concentration in both x and y directions at each point. (d) From mass transport calculations, it can be shown that the concentration 'flux' (amount of product flowing per unit area per unit time) in the two directions at each point are: qx(x,y)=DxC(x,y)+U(x,y)C(x,y)andqy(x,y)=DyC(x,y) Here, D=0.1cm2/s is the mass diffusivity constant and U(x,y)=4y(1y) is the given horizontal flow velocity in cm/s. Determine qx and qy using finite differences and show the 'flow' of reaction products using quivers or streamlines. (e) The net horizontal mass flow rate of the product at every x slice is Q(x)=y=0y=Lyqx(x,y)dy Determine Q(x) between x=0.5cm and x=4cm in steps of 0.1cm and plot it. Comment on how you could use this plot to 'design' the length of a channel necessary for a required product flow rate (no calculations necessary; describe in words)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


