Please complete the method findcombination at the end.

Thank you!

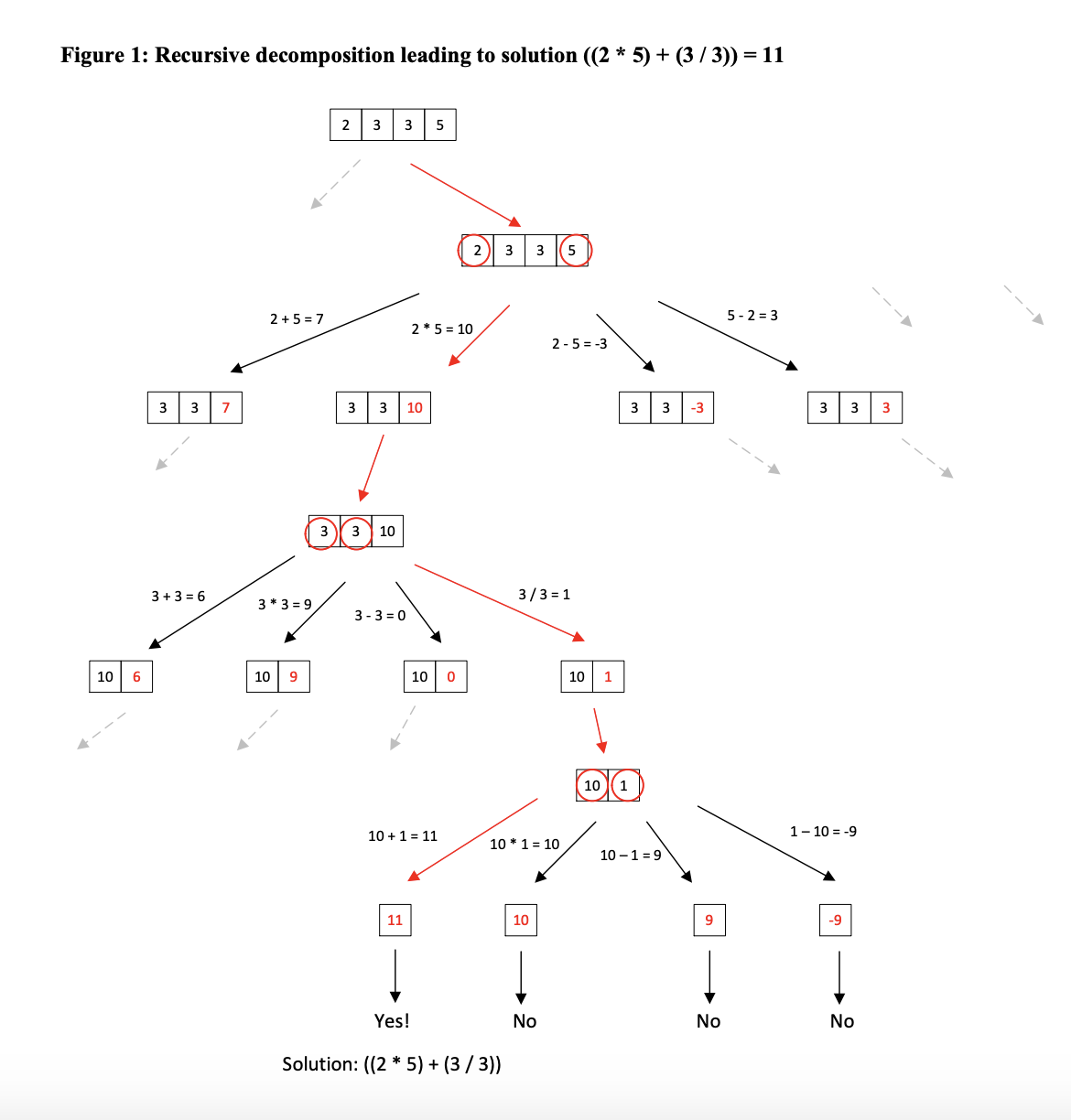
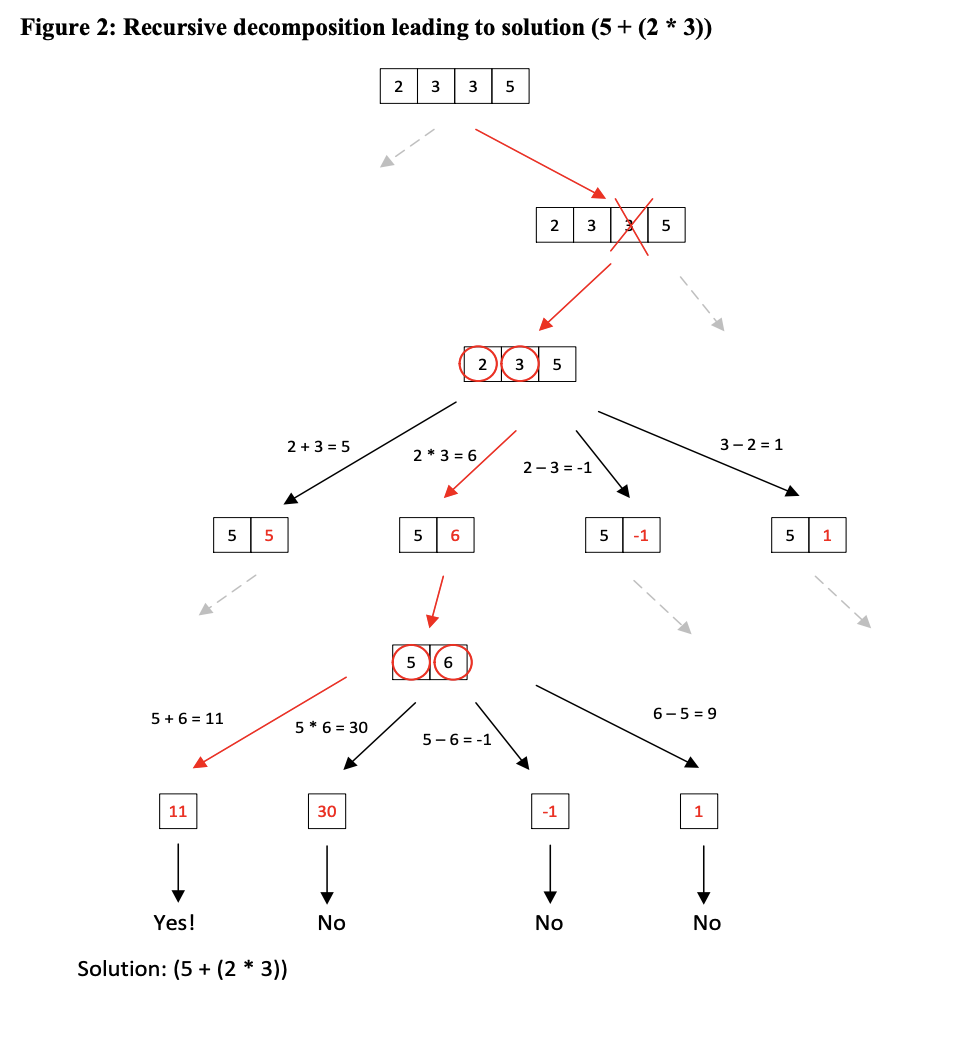
Overview This is a short assignment to have some fun and give you some practice with recursion. Your task is to implement the recursive method findCombinations in the class RecursionGame. This is loosely based on a well-known game called the \"twenty-four game\". The idea is that you are given a list of numbers and a target value (in the traditional form of the game, the target value is always 24). You must combine your numbers using addition, subtraction, multiplication, and division to obtain the target (implicitly you are also using parentheses since you can group the operations). For example, suppose your list of numbers is 2, 3, 4, 5, with a target value of 2 1. Some possible solutions would be ((5 2) * (3 + 4)), ((3 2) + (4 * 5)), or (3 * (2 + 5)). (Note that in our version of the rules, you are not required to use all the numbers, and division is only allowed when there is no remainder. This is different from the traditional version.) The goal of the findCombinations method is to create a list containing all possible solutions, represented as strings. It is ok for the list to contain duplicates and the results do not need to be in any order. Please note, for example, that we regard \"(3 * (2 + 5))\" and \"(3 * (5 + 2))\" as dgferent solutions (this simplies things in the long run). The search for solutions to the twenty-four game is similar, in the sense that recursion is used to explore a tree-like structure representing all possible combinations of the numbers with arithmetic operations. In the case of searching a le hierarchy, the "tree" actually exists on your hard drive, but in the case of the twenty-four game, the "tree" is conceptual. The gures on the following pages illustrate this. To descend down branches of this conceptual tree of possible combinations, we need to decompose the problem into smaller sub-problems so that recursion can be used. There are two possible ways to reduce the problem to a smaller sub-problem. 3) Choose two numbers a and b in the list, remove them om the list, and replace them with a single numbera +3), 13 +a, a *b, b *a, ab, ba, a/b, orb/a. Thisreducesthe listsizeby 1. b) Choose a single number in the list, and remove it. This allows us to find solutions in which not all the numbers are used; again the list size is reduced by 1. The base case is easy: if you have a list of numbers of size 1, you can just check whether that value is equal to the target. The idea is illustrated in the following gures using the list of numbers 2, 3, 3, 5 and the target value 11. In Figure 1, we start by choosing a pair of values om the list. In this example, we are examining the path in which we chose 2 and 5. We can replace the 2 and the 5 with 2 + 5, 2 * 5, 2 5, or 5 2. The possible division expressions 2 I 5 and 5 l 2 are disallowed because both have a nonzero remainder. This leads to four lists with only three numbers in each. The same strategy can now be recursively applied to each of the three-element lists, and here we examine the branch in which the pair 3, 3 is chosen. These values can be replaced with 3 + 3, 3 * 3, 3 3, or 3 l 3, leading to four lists with only two numbers in each. Again we recursively apply the same strategy. In this case there is only one possible pair to choose, so we replace the 10 and 1 with the possible values 10 +1, 10 * 1, 10 1, and 1 10. Now each subproblem is a list of length 1, so we can directly compare each of the values with the target, 11, and there is one solution. Figure 2 is similar, but also illustrates the fact that we need to allow subproblems that are formed just by removing an element and obtaining a shorter list, in order to obtain a solution that doesn't use all the numbers, such as (5 + (2 * 3)). Figure 1: Recursive decomposition leading to solution ((2 * 5) + (3 / 3)) = 11 2 3 3 5 2 3 3 5 2+5 =7 2 * 5 = 10 5-2=3 2-5=-3 3 3 7 3 3 10 3 3 - 3 3 3 3 3 3 10 3+3 =6 3 * 3 = 9 3/3 =1 3- 3=0 10 6 10 9 0 10 1 10 (1 10 + 1 = 11 10 * 1 = 10 1 - 10 =-9 10-1 =9 11 10 9 -9 Yes! No No No Solution: ((2 * 5) + (3 / 3))Figure 2: Recursive decomposition leading to solution (5 + (2 * 3)) 2 3 3 5 2 3 5 2 3 5 2+ 3 =5 2 * 3 = 6 3-2=1 2-3=-1 5 5 5 6 5 -1 5 1 5 6 5+6 = 11 5 * 6 = 30 6-5=9 5-6=-1 11 30 -1 1 Yes! No + No No Solution: (5 + (2 * 3))Pseudocode if the list has length 1 if the value matches the target add it to the list of results otherwise for each number x in the list create a copy of the list that does not include I nd solutions using that list for each pair of numbers x, y in the list for each allowable arithmetic combination 2 of x and y create a copy of the list without x and y, but with 2 added nd solutions using that list When we say \"each allowable arithmetic combination 2 of x and y\