Please compute the E(x|Y=y) in Example 2.4.10 as shown in the attachment

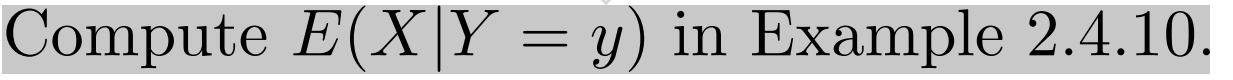
where 1{nsk}(k:,n) is an indicator function taking the value 1 if n S k: and 0 otherwise. Now it is clear that p(k:, n) cannot be factorised, and we see that X and Y are not independent. Of course, this conclusion also follows from the fact that P(X=1)>O,P(Y=2)>0andP(X=1,Y=2)=0. D We can also use joint mass functions to determine the distribution of a sum of two random variables. \fExample 2.4.10. Let (X, Y) have joint mass function C-2-k TL p(k:,n)= ,fork:=1,2,...andn=1,...,k, and suitable constant C. It seems that p(k, n) can be factorised as p(k:, n) = 0219% which would imply that X and Y are independent. However, this is not true. There is dependency between X and Y, which you can see when you look at the values taken by k: and n. In fact, to avoid the range conditions, we could write 02h 190$? 77') I @713\" (k? n)