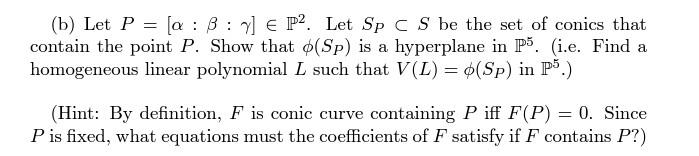
please do it as soon as possible please I will give you upvote

Exercise 5.4 (Curves in P2) Let k be an algebraically closed field. A conic in P2 is a projective algebraic curve of degree 2. Recall that we defined a projective algebraic curve of degree d in P2 to be an equivalence class of degree d homogeneous polynomials under the equivalence relation f~g iff 8 f = lg for some + 0. (b) Let P = [a : 3:] E P2 Let Sp C S be the set of conics that contain the point P. Show that (Sp) is a hyperplane in P5. (i.e. Find a homogeneous linear polynomial L such that V(L) = $(Sp) in P5.) (Hint: By definition, F is conic curve containing Piff F(P) = 0. Since Pis fixed, what equations must the coefficients of F satisfy if F contains P?)