please do it with linear programming. thank you.

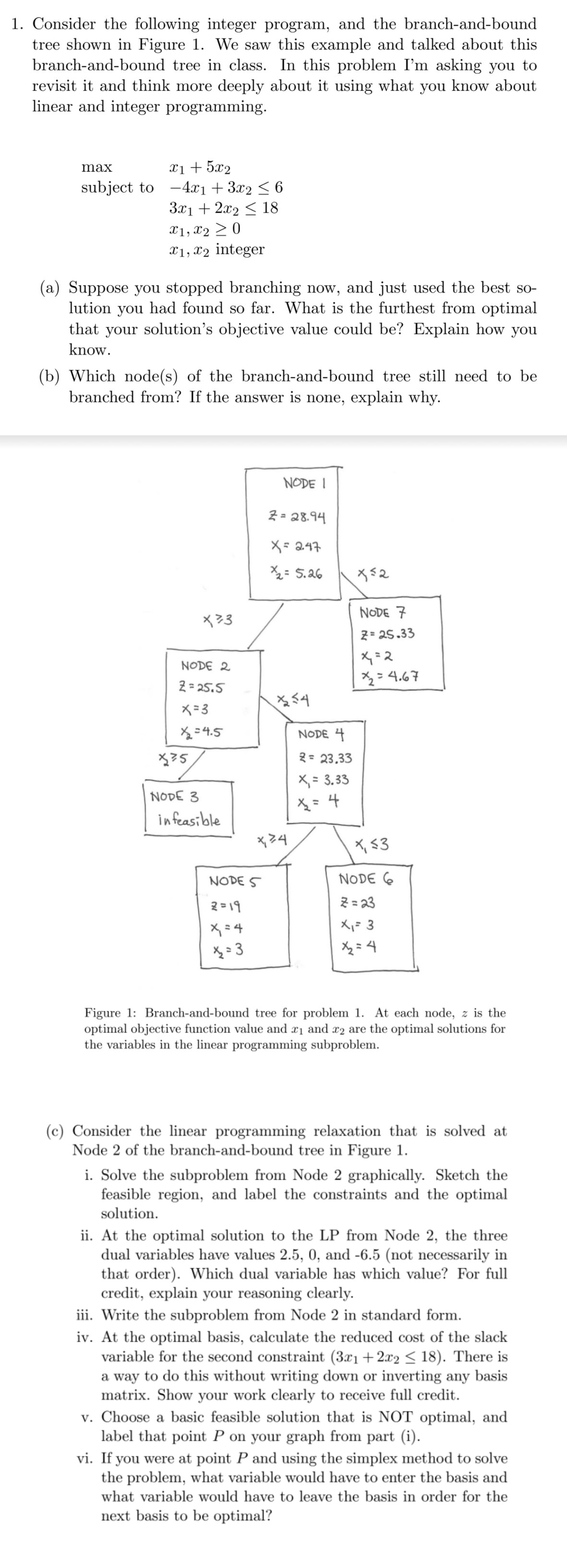
1. Consider the following integer program, and the branch-and-bound tree shown in Figure 1. We saw this example and talked about this branch-and-bound tree in class. In this problem I'm asking you to revisit it and think more deeply about it using what you know about linear and integer programming. max x1 + 51:2 subject to 4x1 + 3:32 3 6 3x1 + 2232 S 18 $1532 2 0 $1, $2 integer (3.) Suppose you stopped branching now, and just used the best so lution you had found so far. What is the furthest from optimal that your solution's objective value could be? Explain how you know. (b) Which node(s) of the branch-and-bound tree still need to be branched from? If the answer is none, explain why. Figure 1: Branch-and-bound tree for problem 1. At each node. 2 is the optimal objective function value and I! and :52 are the optimal solutions for the variables in the linear programming subproblem. (c) Consider the linear programming relaxation that is solved at Node 2 of the branch-andbound tree in Figure 1. i. Solve the subproblem from Node 2 graphically. Sketch the feasible region, and label the constraints and the optimal solution. ii. At the optimal solution to the LP from Node 2, the three dual variables have values 2.5, 0, and -6.5 (not necessarily in that order). Which dual variable has which value? For full credit, explain your reasoning clearly. iii. Write the subproblem from Node 2 in standard form. iv. At the optimal basis, calculate the reduced cost of the slack variable for the second constraint (32:1 + 212 S 18). There is a way to do this without writing down or inverting any basis matrix. Show your work clearly to receive full credit. v. Choose a basic feasible solution that is NOT optimal, and label that point P on your graph from part (i). vi. If you were at point P and using the simplex method to solve the problem, what variable would have to enter the basis and what variable would have to leave the basis in order for the next basis to be optimal