Please do not copy answers from the textbook, please solve and explain yourself in detail.

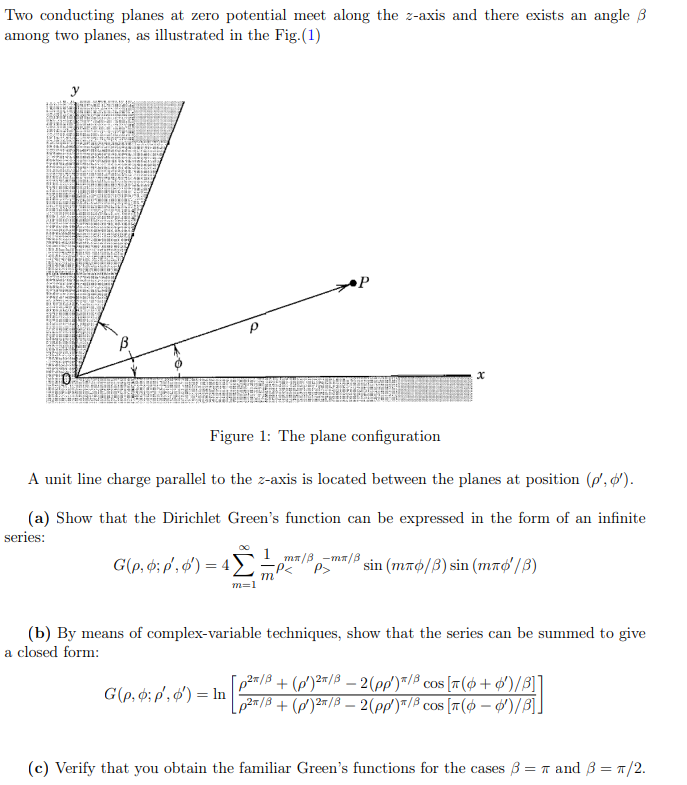
Two conducting planes at zero potential meet along the z-axis and there exists an angle B among two planes, as illustrated in the Fig (1) P x Figure 1: The plane configuration A unit line charge parallel to the z-axis is located between the planes at position (2,6). (a) Show that the Dirichlet Green's function can be expressed in the form of an infinite series: 1 G(2,0; 8,0) = 4 ema/ma/ sin (m$/B) sin (MA/B) -P

m m=1 (b) By means of complex-variable techniques, show that the series can be summed to give a closed form: 02/8 +6)20/8 2(pp)*/ cos [7(6+')/B]] G(2,0;p',6') = In Lp21/B + (!)27/8 2(pp)"/cos [76 - ')/8]] OS (c) Verify that you obtain the familiar Green's functions for the cases B = 1 and B = */2. = Two conducting planes at zero potential meet along the z-axis and there exists an angle B among two planes, as illustrated in the Fig (1) P x Figure 1: The plane configuration A unit line charge parallel to the z-axis is located between the planes at position (2,6). (a) Show that the Dirichlet Green's function can be expressed in the form of an infinite series: 1 G(2,0; 8,0) = 4 ema/ma/ sin (m$/B) sin (MA/B) -P

m m=1 (b) By means of complex-variable techniques, show that the series can be summed to give a closed form: 02/8 +6)20/8 2(pp)*/ cos [7(6+')/B]] G(2,0;p',6') = In Lp21/B + (!)27/8 2(pp)"/cos [76 - ')/8]] OS (c) Verify that you obtain the familiar Green's functions for the cases B = 1 and B = */2. =