PLEASE DO NOT COPY PASTE FROM CHEGG/OTHERWISE I'LL REPORT YOU OR GIVE OU A DISLIKE

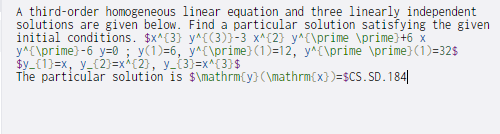
A third-order homogeneous linear equation and three linearly independent solutions are given below. Find a particular solution satisfying the given initial conditions. $x^{3} y^{(3)}-3 x^{2} y^{\prime \prime) +6 x y^{\prime)-6 y=0; y(1)=6, y^{\prime} (1)=12, y^{\prime \prime)(1)=32$ $y_{1}=x, y_{2}=x^{2), y_{3}=x^{3}$ The particular solution is $\mathrm{y}(\mathrm{x})=$CS.SD.184|