Please do not use AI to answer this question, the explanations are often long and incorrect.

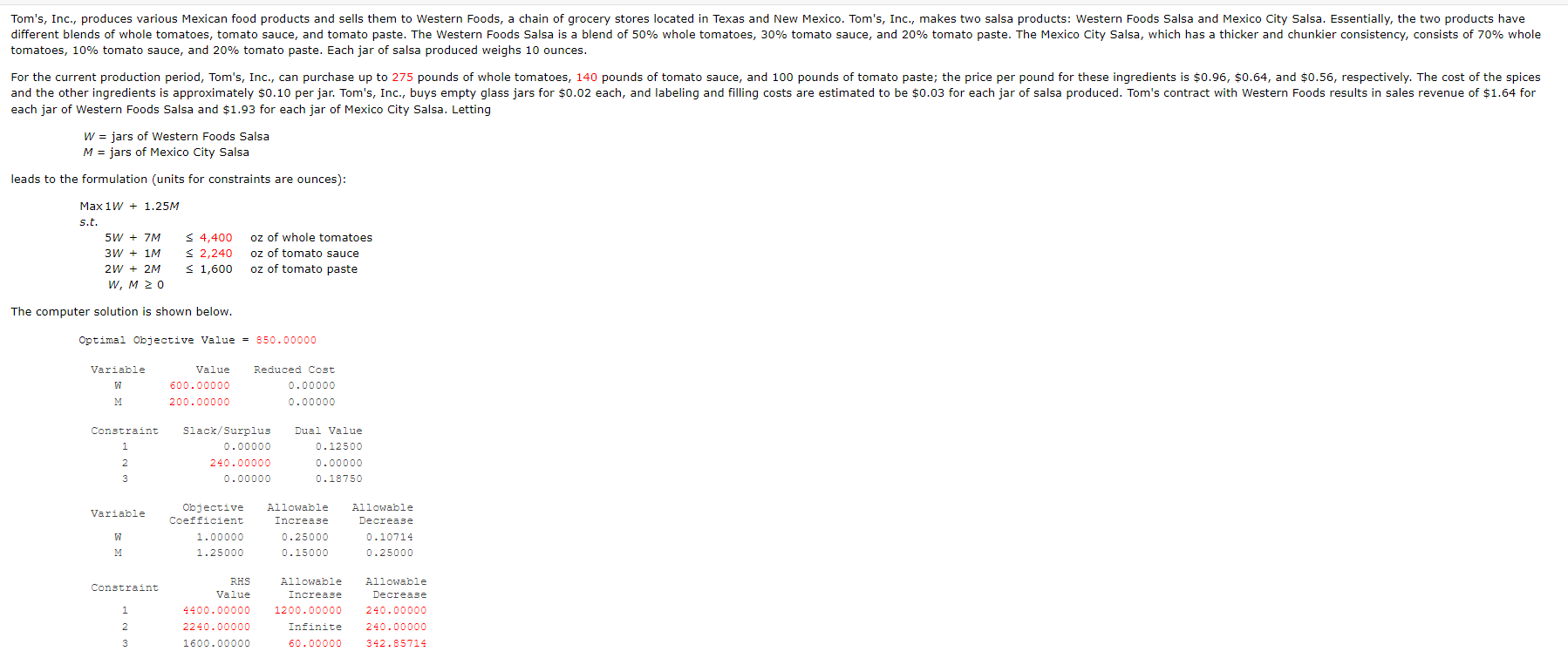
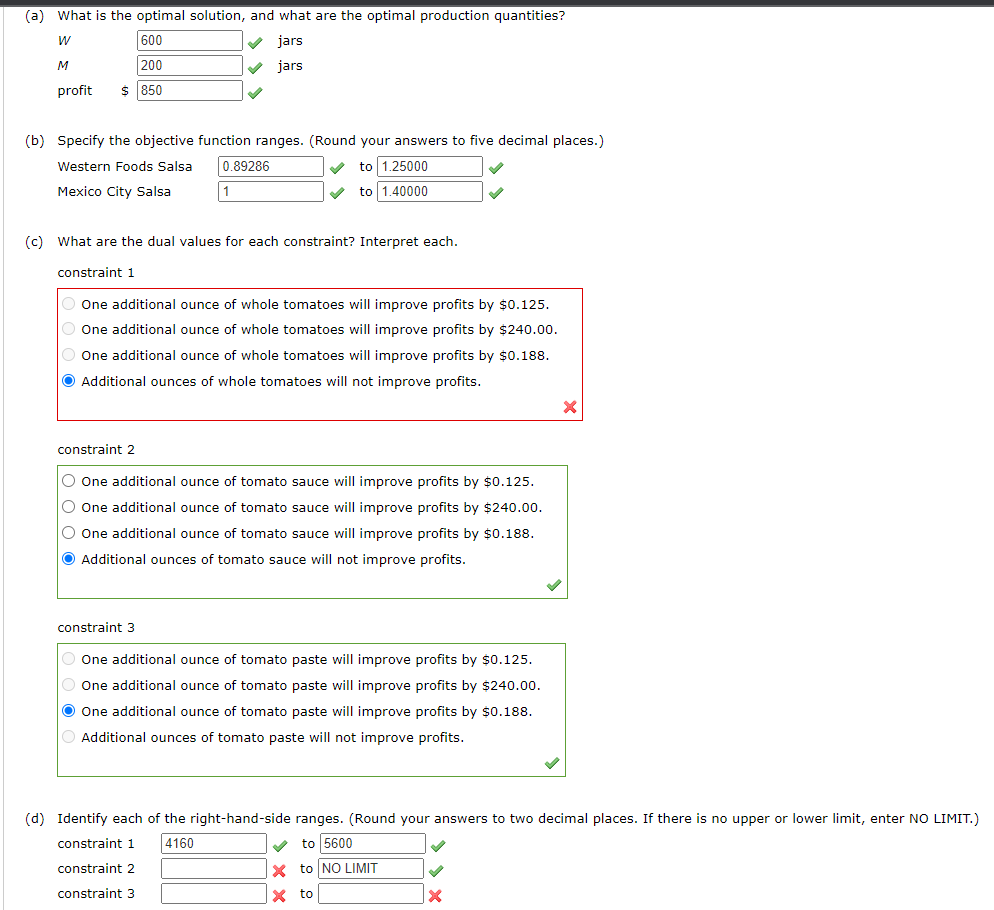
tomatoes, 10% tomato sauce, and 20\% tomato paste. Each jar of salsa produced weighs 10 ounces. each jar of Western Foods Salsa and \$1.93 for each jar of Mexico City Salsa. Letting W=jarsofWesternFoodsSalsaM=jarsofMexicoCitySalsa leads to the formulation (units for constraints are ounces): Max1W+1.25Ms.t.5W+7M2W+2MW,M04,400WW+1M2,2401,600ozofwholetomatoesozoftomatosauceozoftomatopaste Max1W+1.25M s.t. 5W+7M4,400 oz of whole tomatoes 3W+1M2,240 oz of tomato sauce 2W+2M1,600 oz of tomato paste W,M0 The computer solution is shown below. Optimal Objective Value =850.00000 (a) What is the optimal solution, and what are the optimal production quantities? W M jars jars profit $ (b) Specify the objective function ranges. (Round your answers to five decimal places.) Western Foods Salsa to Mexico City Salsa to (c) What are the dual values for each constraint? Interpret each. constraint 1 One additional ounce of whole tomatoes will improve profits by $0.125. One additional ounce of whole tomatoes will improve profits by $240.00. One additional ounce of whole tomatoes will improve profits by $0.188. Additional ounces of whole tomatoes will not improve profits. constraint 2 One additional ounce of tomato sauce will improve profits by $0.125. One additional ounce of tomato sauce will improve profits by $240.00. One additional ounce of tomato sauce will improve profits by $0.188. Additional ounces of tomato sauce will not improve profits. constraint 3 One additional ounce of tomato paste will improve profits by $0.125. One additional ounce of tomato paste will improve profits by $240.00. One additional ounce of tomato paste will improve profits by $0.188. Additional ounces of tomato paste will not improve profits. (d) Identify each of the right-hand-side ranges. (Round your answers to two decimal places. If there is no upper or lower limit, enter NO LIMIT.) constraint 1 to constraint 2 to constraint 3 to tomatoes, 10% tomato sauce, and 20\% tomato paste. Each jar of salsa produced weighs 10 ounces. each jar of Western Foods Salsa and \$1.93 for each jar of Mexico City Salsa. Letting W=jarsofWesternFoodsSalsaM=jarsofMexicoCitySalsa leads to the formulation (units for constraints are ounces): Max1W+1.25Ms.t.5W+7M2W+2MW,M04,400WW+1M2,2401,600ozofwholetomatoesozoftomatosauceozoftomatopaste Max1W+1.25M s.t. 5W+7M4,400 oz of whole tomatoes 3W+1M2,240 oz of tomato sauce 2W+2M1,600 oz of tomato paste W,M0 The computer solution is shown below. Optimal Objective Value =850.00000 (a) What is the optimal solution, and what are the optimal production quantities? W M jars jars profit $ (b) Specify the objective function ranges. (Round your answers to five decimal places.) Western Foods Salsa to Mexico City Salsa to (c) What are the dual values for each constraint? Interpret each. constraint 1 One additional ounce of whole tomatoes will improve profits by $0.125. One additional ounce of whole tomatoes will improve profits by $240.00. One additional ounce of whole tomatoes will improve profits by $0.188. Additional ounces of whole tomatoes will not improve profits. constraint 2 One additional ounce of tomato sauce will improve profits by $0.125. One additional ounce of tomato sauce will improve profits by $240.00. One additional ounce of tomato sauce will improve profits by $0.188. Additional ounces of tomato sauce will not improve profits. constraint 3 One additional ounce of tomato paste will improve profits by $0.125. One additional ounce of tomato paste will improve profits by $240.00. One additional ounce of tomato paste will improve profits by $0.188. Additional ounces of tomato paste will not improve profits. (d) Identify each of the right-hand-side ranges. (Round your answers to two decimal places. If there is no upper or lower limit, enter NO LIMIT.) constraint 1 to constraint 2 to constraint 3 to