Please, do notice that this question has 2 parts.

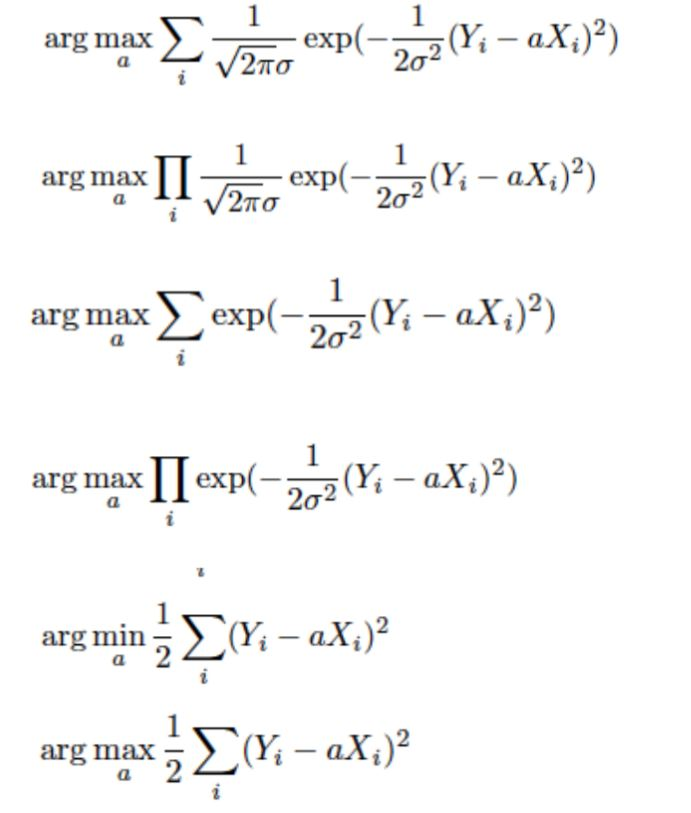
23. Consider real-valued variables X and Y. The Y variable is generated, conditional on X, from the following process: 2 ~ N(0,0 ) where every is an independent variable, called a noise term, which is drawn from a Gaussian distribution with mean 0 and standard deviation . This is a one-feature linear regression model, where a is the only weight parameter. The conditional probability of Y has distribution p(YX,a) ~ N(,2), so it can be written as. Answer the following questions, Assume we have a training dataset of n pairs (Xi, Yi) for i 1.. n, and s known Which ones of the following equations correctly represent the maximum likelihood problem for estimating a? Say yes or no to each one. More than one of them should have the answer "yes." (3 points) 2 2 arg max exp((V, -ax 2 exp (-20 2 arg max !! V2 exp(-22 arg max expi arg max exp(-2-2 ( arg min (Y;-ax.) arg max) Y_aXi) Derive the maximum likelihood estimate (MLE) of the parameter a in terms of the training example Xi 's and Yi 's. I recommend you start with the simplest form of the problem you found above. For example, you may choose to derive the MLE for the following function F(a): ,0. aXi)2 and minimize F. (2 points) ii. 23. Consider real-valued variables X and Y. The Y variable is generated, conditional on X, from the following process: 2 ~ N(0,0 ) where every is an independent variable, called a noise term, which is drawn from a Gaussian distribution with mean 0 and standard deviation . This is a one-feature linear regression model, where a is the only weight parameter. The conditional probability of Y has distribution p(YX,a) ~ N(,2), so it can be written as. Answer the following questions, Assume we have a training dataset of n pairs (Xi, Yi) for i 1.. n, and s known Which ones of the following equations correctly represent the maximum likelihood problem for estimating a? Say yes or no to each one. More than one of them should have the answer "yes." (3 points) 2 2 arg max exp((V, -ax 2 exp (-20 2 arg max !! V2 exp(-22 arg max expi arg max exp(-2-2 ( arg min (Y;-ax.) arg max) Y_aXi) Derive the maximum likelihood estimate (MLE) of the parameter a in terms of the training example Xi 's and Yi 's. I recommend you start with the simplest form of the problem you found above. For example, you may choose to derive the MLE for the following function F(a): ,0. aXi)2 and minimize F. (2 points)