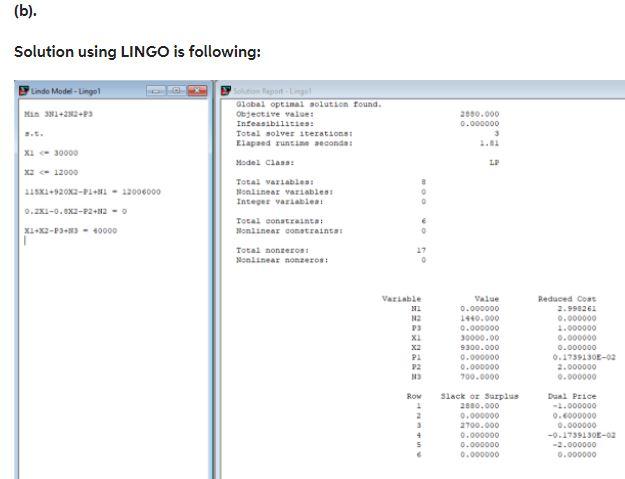
Question: Please do parts c) and d) using LINGO . The answer for parts a) and b) are included with the question below. A license to
Please do parts c) and d) using LINGO. The answer for parts a) and b) are included with the question below.



Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


