please do question b, explain step by step and show work. thank you.

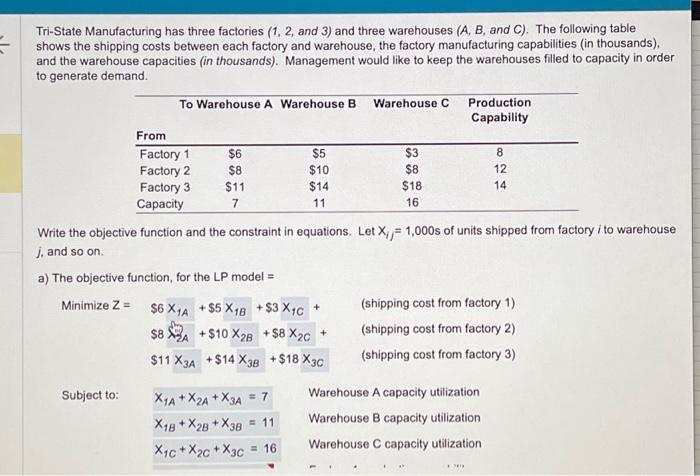
Tri-State Manufacturing has three factories (1,2, and 3) and three warehouses (A,B, and C). The following table shows the shipping costs between each factory and warehouse, the factory manufacturing capabilities (in thousands), and the warehouse capacities (in thousands). Management would like to keep the warehouses filled to capacity in order to generate demand. Write the objective function and the constraint in equations. Let Xij=1,000 s of units shipped from factory i to warehouse j, and so on. a) The objective function, for the LP model = MinimizeZ=$6X1A+$5X1B+$3X1C+$8X2A+$10X2B+$8X2C+$11X3A+$14x3B+$18X3C(shippingcostfromfactory1)(shippingcostfromfactory2)(shippingcostfromfactory3) (shipping cost from factory 3 ) Subject to: x1A+x2A+x3A=7x1B+x2B+x3B=11x1C+x2C+x3C=16 Warehouse A capacity utilization Warehouse B capacity utilization Warehouse C capacity utilization Write the objective function and the constraint in equations. Let Xij=1,000 s of units shipped from factory i to warehouse j, and so on. a) The objective function, for the LP model = MinimizeZ=$6X1A+$5X1B+$3X1C+(shippingcostfromfactory1)$8X2A+$10X2B+$8X2C+(shippingcostfromfactory2)$11X3A+$14X3B+$18X3C(shippingcostfromfactory3) Subject to: X1A+X2A+X3A=7 Warehouse A capacity utilization X1B+X2B+X3B=11WarehouseBcapacityutilization X1C+X2C+X3C=16WarehouseCcapacityutilization X1A+X1B+X1C8 Factory 1 production capability X2A+X2B+X2C12 Factory 2 production capability X3A+X3B+X3C14 Factory 3 production capability For all Xij0 non negativity condition b) Using a computer software for solving LP, the optimal solution achieved is: Total shipping costs (in thousands) =$ (enter your response as a whole number)