Please explain all answers clearly

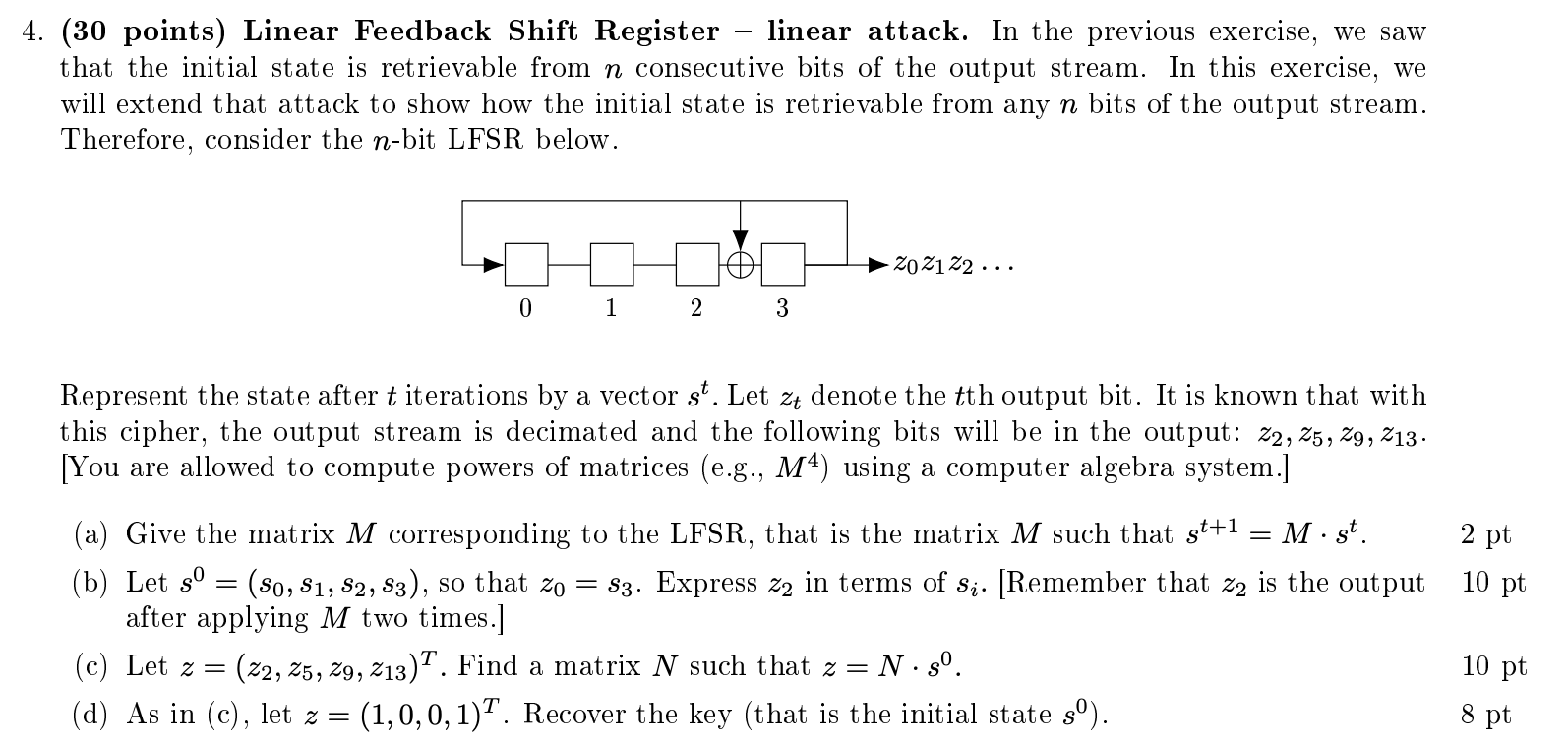
4. (30 points) Linear Feedback Shift Register linear attack. In the previous exercise, we saw that the initial state is retrievable from n consecutive bits of the output stream. In this exercise, we will extend that attack to show how the initial state is retrievable from any n bits of the output stream. Therefore, consider the n-bit LFSR below. 20 21 22 ... 0 1 2 3 Represent the state after t iterations by a vector st. Let zt denote the tth output bit. It is known that with this cipher, the output stream is decimated and the following bits will be in the output: 22, 25, 29, 213. [You are allowed to compute powers of matrices (e.g., M4) using a computer algebra system.] = 2 pt 10 pt (a) Give the matrix M corresponding to the LFSR, that is the matrix M such that st+1 M st. (b) Let s = (S0, S1, S2, S3), so that zo = 83. Express z2 in terms of s. [Remember that za is the output after applying M two times.] (c) Let z = (22, 25, 29, 213). Find a matrix N such that z = = N.80. (d) As in (c), let z = (1,0,0,1)). Recover the key (that is the initial state s). 10 pt 8 pt 4. (30 points) Linear Feedback Shift Register linear attack. In the previous exercise, we saw that the initial state is retrievable from n consecutive bits of the output stream. In this exercise, we will extend that attack to show how the initial state is retrievable from any n bits of the output stream. Therefore, consider the n-bit LFSR below. 20 21 22 ... 0 1 2 3 Represent the state after t iterations by a vector st. Let zt denote the tth output bit. It is known that with this cipher, the output stream is decimated and the following bits will be in the output: 22, 25, 29, 213. [You are allowed to compute powers of matrices (e.g., M4) using a computer algebra system.] = 2 pt 10 pt (a) Give the matrix M corresponding to the LFSR, that is the matrix M such that st+1 M st. (b) Let s = (S0, S1, S2, S3), so that zo = 83. Express z2 in terms of s. [Remember that za is the output after applying M two times.] (c) Let z = (22, 25, 29, 213). Find a matrix N such that z = = N.80. (d) As in (c), let z = (1,0,0,1)). Recover the key (that is the initial state s). 10 pt 8 pt