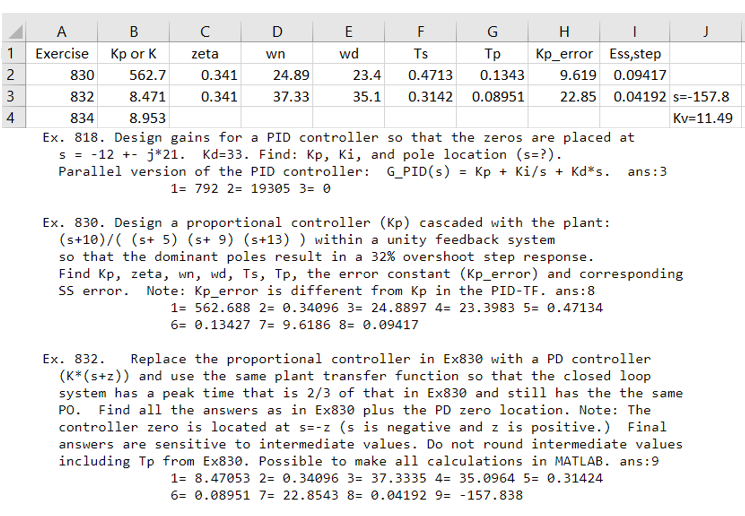PLEASE EXPLAIN HOW CAN WE APPROACH TO Kp_error TO 22.85 IN THIS PROBLEM. ABOVESHEET IS THE ANSWERS

JUST WANT TO SLOVE FOR Kp_error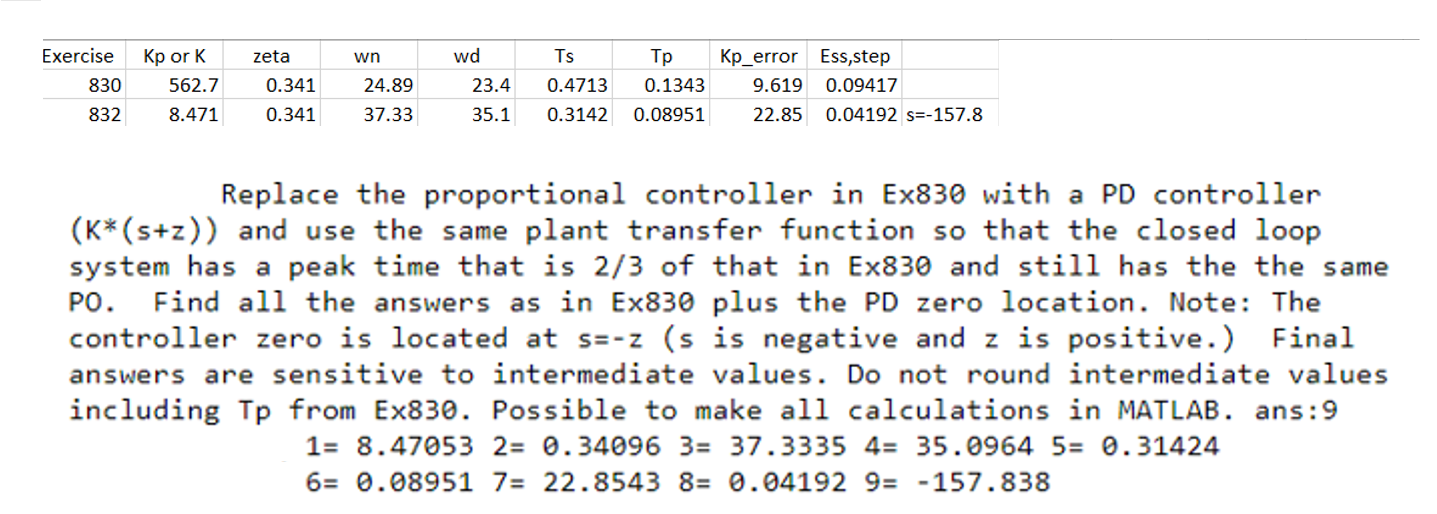

wn 2 1 2 3 4 A B D E F G H Exercise Kp ork zeta wd TS Kp_error Ess,step 830 562.7 0.341 24.89 23.4 0.4713 0.1343 9.619 0.09417 832 8.471 0.341 37.33 35.1 0.3142 0.08951 22.85 0.04192 s=-157.8 834 8.953 Kv=11.49 Ex. 818. Design gains for a PID controller so that the zeros are placed at S = -12 +- j*21. Kd=33. Find: kp, Ki, and pole location (s=?). Parallel version of the PID controller: G_PID(s) = Kp + Ki/s + Kd*s. ans :3 1= 792 2= 19305 3= 0 Ex. 830. Design a proportional controller (KP) cascaded with the plant: (s+10)/( (s+ 5) (s+ 9) (s+13)) within a unity feedback system so that the dominant poles result in a 32% overshoot step response. Find Kp, zeta, wn, wd, Ts, Tp, the error constant (Kp_error) and corresponding SS error. Note: Kp_error is different from Kp in the PID-TF. ans: 8 1= 562.688 2= 0.34096 3= 24.8897 4= 23.3983 5= 0.47134 6= 0.13427 7= 9.6186 8= 0.09417 Ex. 832. Replace the proportional controller in Ex830 with a PD controller (K* (s+z)) and use the same plant transfer function so that the closed loop system has a peak time that is 2/3 of that in Ex830 and still has the the same PO. Find all the answers as in Ex830 plus the PD zero location. Note: The controller zero is located at s=-z (s is negative and z is positive.) Final answers are sensitive to intermediate values. Do not round intermediate values including Tp from Ex830. Possible to make all calculations in MATLAB. ans:9 1= 8.47053 2= 0.34096 3= 37.3335 4= 35.0964 5= 0.31424 6= 0.08951 7= 22.8543 8= 0.04192 9= -157.838 zeta wn Exercise 830 832 Kp or K 562.7 8.471 0.341 24.89 37.33 wd 23.4 35.1 Ts 0.4713 0.3142 0.1343 0.08951 Kp_error Ess,step 9.619 0.09417 22.85 0.04192 s=-157.8 0.341 Replace the proportional controller in Ex830 with a PD controller (K*(s+z)) and use the same plant transfer function so that the closed loop system has a peak time that is 2/3 of that in Ex830 and still has the the same PO. Find all the answers as in Ex830 plus the PD zero location. Note: The controller zero is located at s=-z (s is negative and z is positive.) Final answers are sensitive to intermediate values. Do not round intermediate values including Tp from Ex830. Possible to make all calculations in MATLAB. ans: 9 1= 8.47053 2= 0.34096 3= 37.3335 4= 35.0964 5= 0.31424 6= 0.08951 7= 22.8543 8= 0.04192 9= -157.838 wn 2 1 2 3 4 A B D E F G H Exercise Kp ork zeta wd TS Kp_error Ess,step 830 562.7 0.341 24.89 23.4 0.4713 0.1343 9.619 0.09417 832 8.471 0.341 37.33 35.1 0.3142 0.08951 22.85 0.04192 s=-157.8 834 8.953 Kv=11.49 Ex. 818. Design gains for a PID controller so that the zeros are placed at S = -12 +- j*21. Kd=33. Find: kp, Ki, and pole location (s=?). Parallel version of the PID controller: G_PID(s) = Kp + Ki/s + Kd*s. ans :3 1= 792 2= 19305 3= 0 Ex. 830. Design a proportional controller (KP) cascaded with the plant: (s+10)/( (s+ 5) (s+ 9) (s+13)) within a unity feedback system so that the dominant poles result in a 32% overshoot step response. Find Kp, zeta, wn, wd, Ts, Tp, the error constant (Kp_error) and corresponding SS error. Note: Kp_error is different from Kp in the PID-TF. ans: 8 1= 562.688 2= 0.34096 3= 24.8897 4= 23.3983 5= 0.47134 6= 0.13427 7= 9.6186 8= 0.09417 Ex. 832. Replace the proportional controller in Ex830 with a PD controller (K* (s+z)) and use the same plant transfer function so that the closed loop system has a peak time that is 2/3 of that in Ex830 and still has the the same PO. Find all the answers as in Ex830 plus the PD zero location. Note: The controller zero is located at s=-z (s is negative and z is positive.) Final answers are sensitive to intermediate values. Do not round intermediate values including Tp from Ex830. Possible to make all calculations in MATLAB. ans:9 1= 8.47053 2= 0.34096 3= 37.3335 4= 35.0964 5= 0.31424 6= 0.08951 7= 22.8543 8= 0.04192 9= -157.838 zeta wn Exercise 830 832 Kp or K 562.7 8.471 0.341 24.89 37.33 wd 23.4 35.1 Ts 0.4713 0.3142 0.1343 0.08951 Kp_error Ess,step 9.619 0.09417 22.85 0.04192 s=-157.8 0.341 Replace the proportional controller in Ex830 with a PD controller (K*(s+z)) and use the same plant transfer function so that the closed loop system has a peak time that is 2/3 of that in Ex830 and still has the the same PO. Find all the answers as in Ex830 plus the PD zero location. Note: The controller zero is located at s=-z (s is negative and z is positive.) Final answers are sensitive to intermediate values. Do not round intermediate values including Tp from Ex830. Possible to make all calculations in MATLAB. ans: 9 1= 8.47053 2= 0.34096 3= 37.3335 4= 35.0964 5= 0.31424 6= 0.08951 7= 22.8543 8= 0.04192 9= -157.838