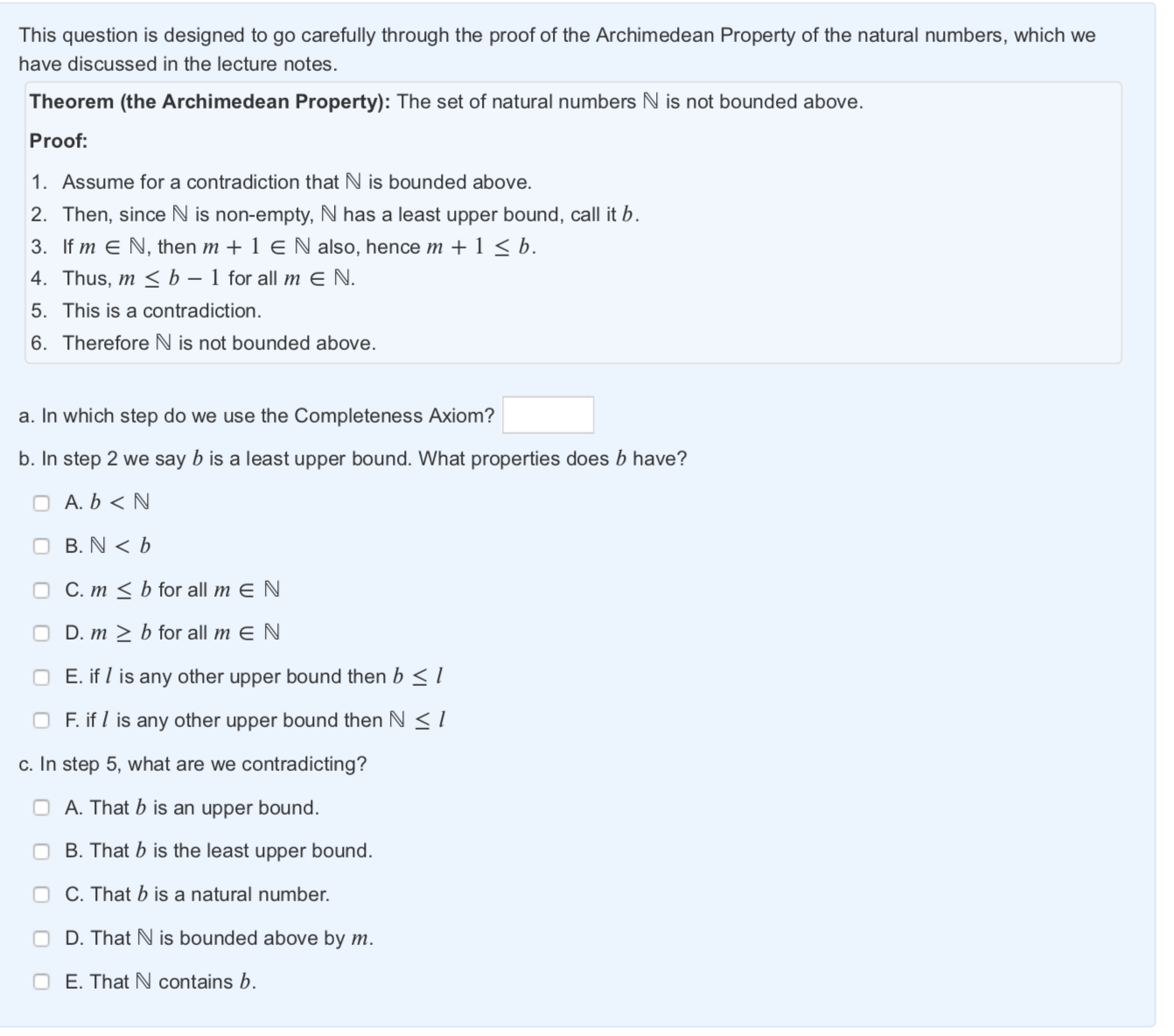
Question: Please explain step by step, thanks! This question is designed to go carefully through the proof of the Archimedean Property of the natural numbers, which

Please explain step by step, thanks!

This question is designed to go carefully through the proof of the Archimedean Property of the natural numbers, which we have discussed in the lecture notes. Theorem (the Archimedean Property): The set of natural numbers N is not bounded above. Proof: 1. Assume for a contradiction that N is bounded above. 2. Then, since N is non-empty, N has a least upper bound, call it b. 3. If m E N, then m + 1 E N also, hence m + 1 5 b. 4. Thus, m b for all m E N O E. if I is any other upper bound then b 5 1 O F. if I is any other upper bound then N

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

All the required info is attached. Make sure to address the the requirement stated 1-4. any question let me know. Case Study: Tarheel Textiles (5-7 pages) (The IIA Research Foundation, Case Studies...

Assignment #1 Directions: Read and answer the questions below.This assignment is to be completed in two steps.Step One of the assignment is due on October 7, 2021, before class.For Step One, you are...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Chapter 7 Revising and Presenting Your Writing I'm not a very good writer, but I'm an excellent rewriter. James A. Michener Half my life is an act of revision. John Irving Getting Started INT RODU CT...

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

In this question assume that p and q are atomic formulae. (a) Compare and contrast path formulae and state formulae in temporal logic. [4 marks] (b) Describe and contrast the meanings of F(G p) and...

I am so lost with all of this and the worst part it is due in an hour and a half. I don't know what to do please help. In this course you will have the opportunity to apply the concepts learned to a...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

If you could please help me with the following audit report case that is attached. Case Study: Tarheel Textiles (4 pages) (The IIA Research Foundation, Case Studies in Internal Auditing, Volume 4,...

A former chairman, CFO, and controller of Donnkenny, Inc., an apparel company that makes sportswear for Pierre Cardin and Victoria Jones, pleaded guilty to financial statement fraud. These managers...

Suppose the heavily doped p-GaAs described above is now sandwiched between AIAs barrier layers to form a single quantum well (SQW) structure with a well width, L= 100 nm. Once again assume for...

9 : 4 3 4 1 Return to Reading 5 5 8 2 7 % A new partner can be admitted to an existing partnership in which of the following ways? ( Check all that apply. ) Select All That Apply Withdrawing cash...

The test statistic is (Type an integer or a decimal. Do not round.) The critical value is (Round to three decimal places as needed.) State the conclusion. Ho. There sufficient evidence to warrant...