Please explain the steps too!

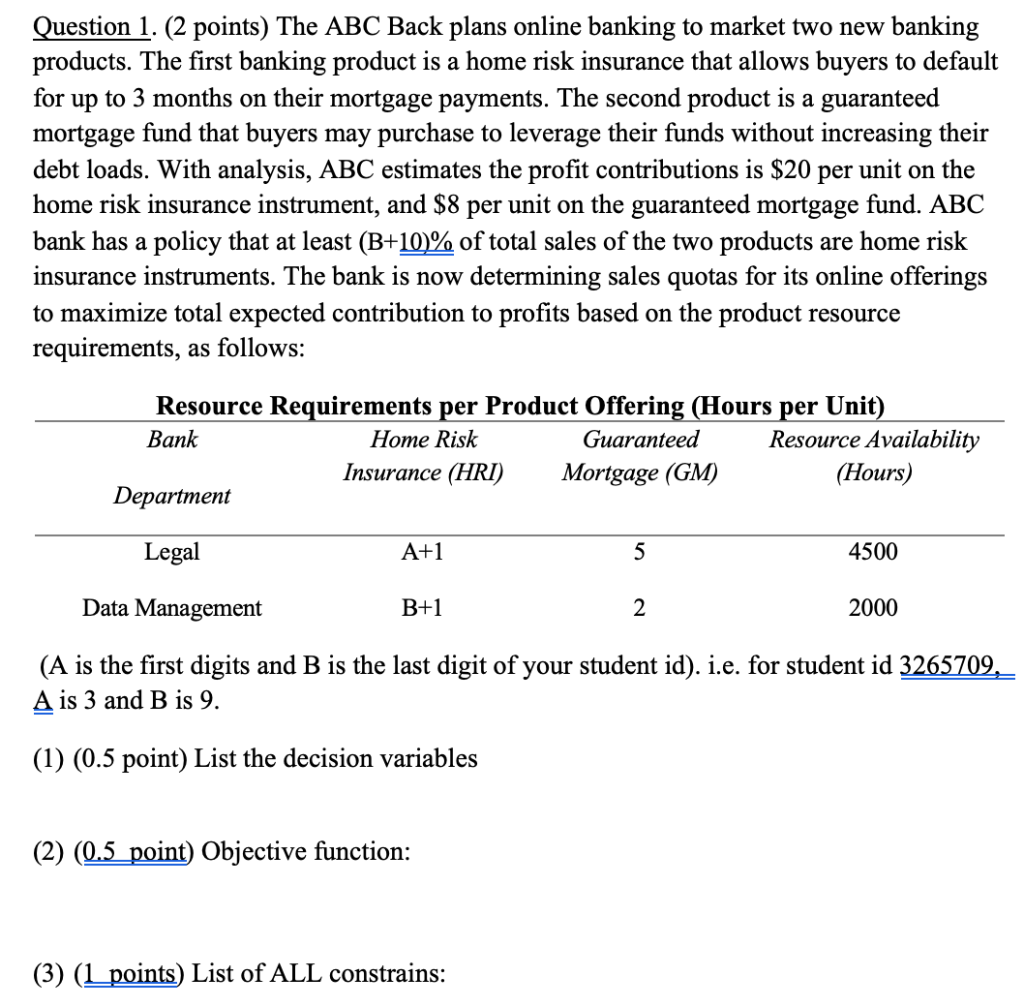
Question 1. (2 points) The ABC Back plans online banking to market two new banking products. The first banking product is a home risk insurance that allows buyers to default for up to 3 months on their mortgage payments. The second product is a guaranteed mortgage fund that buyers may purchase to leverage their funds without increasing their debt loads. With analysis, ABC estimates the profit contributions is $20 per unit on the home risk insurance instrument, and $8 per unit on the guaranteed mortgage fund. ABC bank has a policy that at least (B+10)% of total sales of the two products are home risk insurance instruments. The bank is now determining sales quotas for its online offerings to maximize total expected contribution to profits based on the product resource requirements, as follows: (A is the first digits and B is the last digit of your student id). i.e. for student id 3265709, A is 3 and B is 9 . (1) (0.5 point) List the decision variables (2) ( 0.5point)Objectivefunction: (3) ( 1 points ) List of ALL constrains: 2. (1.5 points) Consider the following linear programming problem (in LINGO style) with two products: Max 11+4x2 s.t. x1+2x2=1 end and the printout is (1) (0.5 point) What is the optimal solution \& what is the associated optimal result? (2) (0.5 point) What is the reduced cost for the X1 and what does it mean? (3) (0.5 point) What is the dual price for the first constraint and what does it mean? Question 3 ( 2.5 points): Consider the following linear programming problem: Minimize X2Y Subject to (1) 2X2Y4 (2) X+Y4 (3) 2X5 (4) Y4 X,Y0 (1) (0.5 point) Clearly show the feasible region and gradient on the graph. (2) (0.5 point) Clearly show gradient on the graph. (3) (0.5 point) Use the graphical solution technique to determine the point for optimal solution. Clearly show the optimal point on the graph and list simultaneous equation to get optimal solution. What is the value of the objective function at optimum? (Show your calculations). (4) (0.5 point) Explain in one sentence how the gradient of the objective function changes of the coefficient of x2 decreases. (5) (0.5 point) If the second constrain is changed to x+2Y5, how many optimal solution(s)? (Show on your graph for (1) and (2))