Please fill in the blanks, drop downs and the ones that require numbers. The numbers in the table are correct.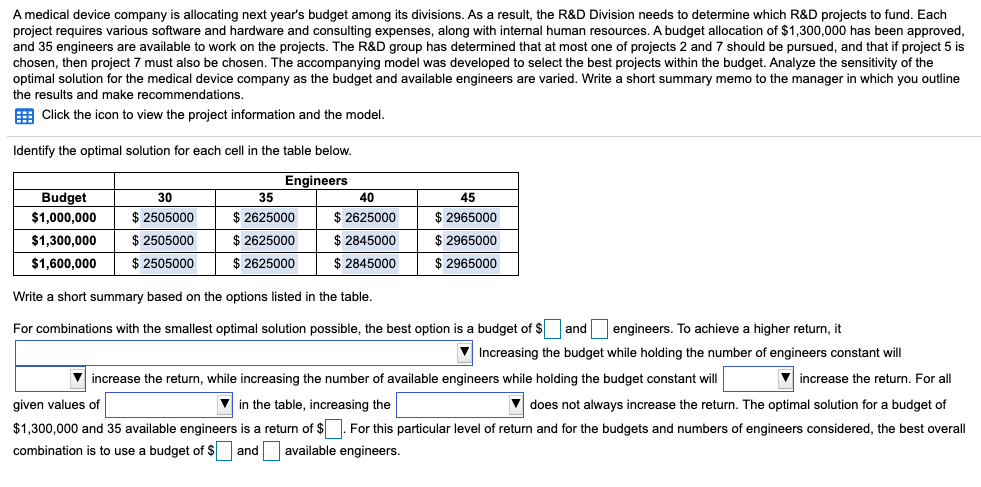

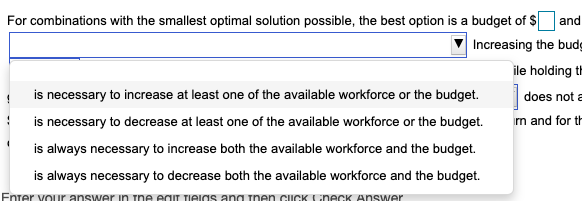
A medical device company is allocating next year's budget among its divisions. As a result, the R&D Division needs to determine which R&D projects to fund. Each project requires various software and hardware and consulting expenses, along with internal human resources. A budget allocation of $1,300,000 has been approved, and 35 engineers are available to work on the projects. The R&D group has determined that at most one of projects 2 and 7 should be pursued, and that if project 5 is chosen, then project 7 must also be chosen. The accompanying model was developed to select the best projects within the budget. Analyze the sensitivity of the optimal solution for the medical device company as the budget and available engineers are varied. Write a short summary memo to the manager in which you outline the results and make recommendations. Click the icon to view the project information and the model. Identify the optimal solution for each cell in the table below. Budget $1,000,000 $1,300,000 $1,600,000 30 $ 2505000 $ 2505000 $ 2505000 Engineers 35 40 $ 2625000 $ 2625000 $ 2625000 $ 2845000 $ 2625000 $ 2845000 45 $ 2965000 $ 2965000 $ 2965000 Write a short summary based on the options listed in the table. For combinations with the smallest optimal solution possible, the best option is a budget of $and engineers. To achieve a higher return, it Increasing the budget while holding the number of engineers constant will increase the return, while increasing the number of available engineers while holding the budget constant will increase the return. For all given values of in the table, increasing the V does not always increase the return. The optimal solution for a budget of $1,300,000 and 35 available engineers is a return of $. For this particular level of return and for the budgets and numbers of engineers considered, the best overall combination is to use a budget of $ and available engineers. For combinations with the smallest optimal solution possible, the best option is a budget of $and Increasing the bud ile holding th is necessary to increase at least one of the available workforce or the budget. does not a is necessary to decrease at least one of the available workforce or the budget. m and forth is always necessary to increase both the available workforce and the budget. is always necessary to decrease both the available workforce and the budget. Enter your answer in ne eau Telas ang nen CUICK Check Answer will increase t etu tion ver: always jer: not always increase always va not always and urn of $ ist available number of engineers budget Mer in the edit fields and then click Ch nis ir th ers budget number of engineers A medical device company is allocating next year's budget among its divisions. As a result, the R&D Division needs to determine which R&D projects to fund. Each project requires various software and hardware and consulting expenses, along with internal human resources. A budget allocation of $1,300,000 has been approved, and 35 engineers are available to work on the projects. The R&D group has determined that at most one of projects 2 and 7 should be pursued, and that if project 5 is chosen, then project 7 must also be chosen. The accompanying model was developed to select the best projects within the budget. Analyze the sensitivity of the optimal solution for the medical device company as the budget and available engineers are varied. Write a short summary memo to the manager in which you outline the results and make recommendations. Click the icon to view the project information and the model. Identify the optimal solution for each cell in the table below. Budget $1,000,000 $1,300,000 $1,600,000 30 $ 2505000 $ 2505000 $ 2505000 Engineers 35 40 $ 2625000 $ 2625000 $ 2625000 $ 2845000 $ 2625000 $ 2845000 45 $ 2965000 $ 2965000 $ 2965000 Write a short summary based on the options listed in the table. For combinations with the smallest optimal solution possible, the best option is a budget of $and engineers. To achieve a higher return, it Increasing the budget while holding the number of engineers constant will increase the return, while increasing the number of available engineers while holding the budget constant will increase the return. For all given values of in the table, increasing the V does not always increase the return. The optimal solution for a budget of $1,300,000 and 35 available engineers is a return of $. For this particular level of return and for the budgets and numbers of engineers considered, the best overall combination is to use a budget of $ and available engineers. For combinations with the smallest optimal solution possible, the best option is a budget of $and Increasing the bud ile holding th is necessary to increase at least one of the available workforce or the budget. does not a is necessary to decrease at least one of the available workforce or the budget. m and forth is always necessary to increase both the available workforce and the budget. is always necessary to decrease both the available workforce and the budget. Enter your answer in ne eau Telas ang nen CUICK Check Answer will increase t etu tion ver: always jer: not always increase always va not always and urn of $ ist available number of engineers budget Mer in the edit fields and then click Ch nis ir th ers budget number of engineers