Please fill in the blanks, & true false,

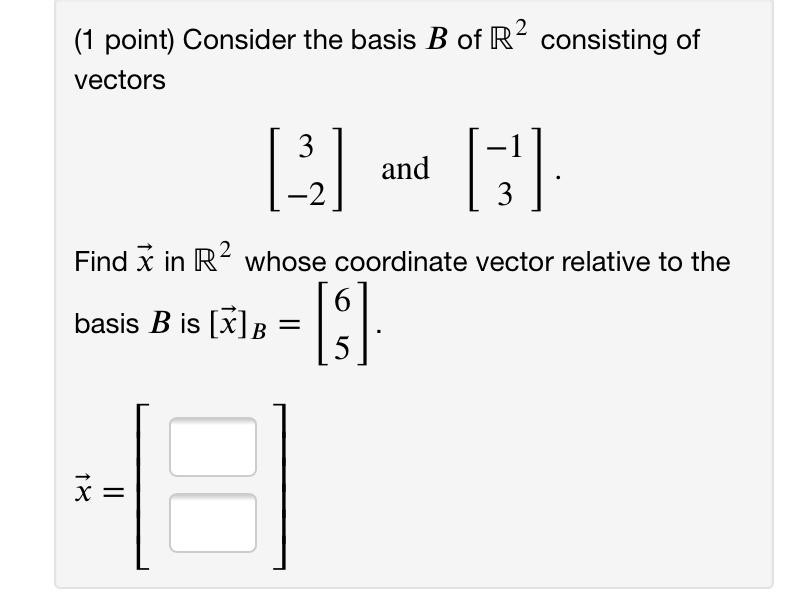
(1 point) Determine if the set of vectors is a basis of R4 . If not, determine the dimension of the subspace spanned by the vectors. a 5 -3 7 o 1 4 -2 -5 1 1 6 { } 2 3 -5 s The dimension of the subspace spanned by the vectors is (1 point) Consider the basis B of [R2 consisting of vectors 3 and _1 . 2 3 Find 35 in R2 whose coordinate vector relative to the basisB is [35]}; = [2]. M II (1 point) Are the following statements true or false? 7 1. If the set of vectors U spans a subspace S , then vectors can be removed from U to create a basis for S ? 2. If the set of vectors U is Iineariy independent in a subspace S then vectors can be added to U to create a basis for S ? 3. If S = span{u1,u2,u3}, then dim(S) = 3 . ? 4. If the set of vectors U spans a subspace S , then vectors can be added to U to create a basis for S ? 5. If the set of vectors U is lineariv independent in a subsoace S then vectors can be removed from U to create a basis for S