Please finish the code in PYTHON:

Compute a reduced QR factorization of the polynomials in the columns of A using the Gram-Schmidt algorithm. The factor Q will be a list of polynomials and R will be a square matrix.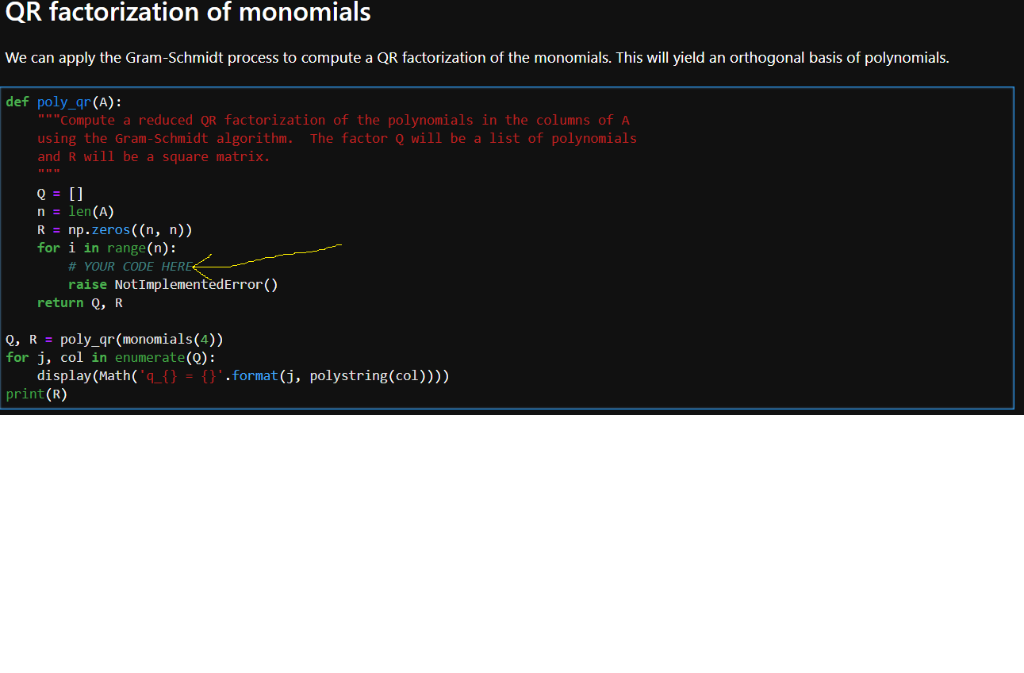

QR factorization of monomials We can apply the Gram-Schmidt process to compute a QR factorization of the monomials. This will yield an orthogonal basis of polynomials. def poly_qr(A) Compute a reduced QR factorization of the polynomials in the columns of A using the Gram-Schmidt algorithm. The factor Q will be a list of polynomials and R will be a square matrix. n -len(A) R np.zeros((n, n)) for i in range(n): # YOUR CODE HERE raise NotImplementedError() return Q, R Q,R-poly_qr(monomials(4)) for j, col in enumerate(Q): print(R) QR factorization of monomials We can apply the Gram-Schmidt process to compute a QR factorization of the monomials. This will yield an orthogonal basis of polynomials. def poly_qr(A) Compute a reduced QR factorization of the polynomials in the columns of A using the Gram-Schmidt algorithm. The factor Q will be a list of polynomials and R will be a square matrix. n -len(A) R np.zeros((n, n)) for i in range(n): # YOUR CODE HERE raise NotImplementedError() return Q, R Q,R-poly_qr(monomials(4)) for j, col in enumerate(Q): print(R)