please fix my mathlab code : $\%$ Parameters

E $=210$e$9$; $\%$ Young's Modulus $($Pa$)$ for steel

R $=0\mathrm{.}013$; $\%$ Outer radius $($m$)$

r $=0\mathrm{.}011$; $\%$ Inner radius $($m$)$

P $=2000$; $\%$ Applied force $($N$)$

L $=1\mathrm{.}0$; $\%$ Length of the beam $($m$)$

d $=0\mathrm{.}75$; $\%$ Distance of force application from the left$-$hand edge $($m$)$

$\%$ Calculate the second moment of area $($I$)$ for a hollow circular cross$-$section

I $=($pi $()/()4)*($R$^(4)-$ r$^(4))$;

$\%$ Define the bending moment M$($x$)$

syms x

M $=$ piecewise$($x $>=0$ & x d$,-$P $*($L $-$ d$)*$ x $()/()$ L$,...$

x $>$ d & x L$,-$P $*$ d $*($L $-$ x$)()/()$ L$)$;

$\%$ Solve EI $*$ d$^(2)($y$)/($d$)$x$^(2)=$ M$($x$)$

syms y$($x$)$

eqn $=$ E $*$ I $*$ diff$($y$,$ x$,2)==$ M;

y$\_($s$)$ol $=$ dsolve$($eqn$)$;

$\%$ Apply boundary conditions: y$(0)=0,$ y$($L$)=0$

C$1=$ dsolve$($eqn$,$ y$(0)==0,$ y$($L$)==0)$;

$\%$ Solve for constants of integration

y$\_($s$)$ol $=$ simplify$($C$1)$;

$\%$ Display results

disp$(\text{'}$Beam Deflection Function, y$($x$)$:$\text{'})$;

disp$($y$\_($s$)$ol$)$;

$\%$ Plot the deflection

fplot$($y$\_($s$)$ol$,[0$ L$])$;

xlabel$(\text{'}$x $($m$)\text{'})$;

ylabel$(\text{'}$Deflection$,$ y$($x$)($m$)\text{'})$;

title$(\text{'}$Deflection of Euler$-$Bernoulli Beam'$)$;

grid on

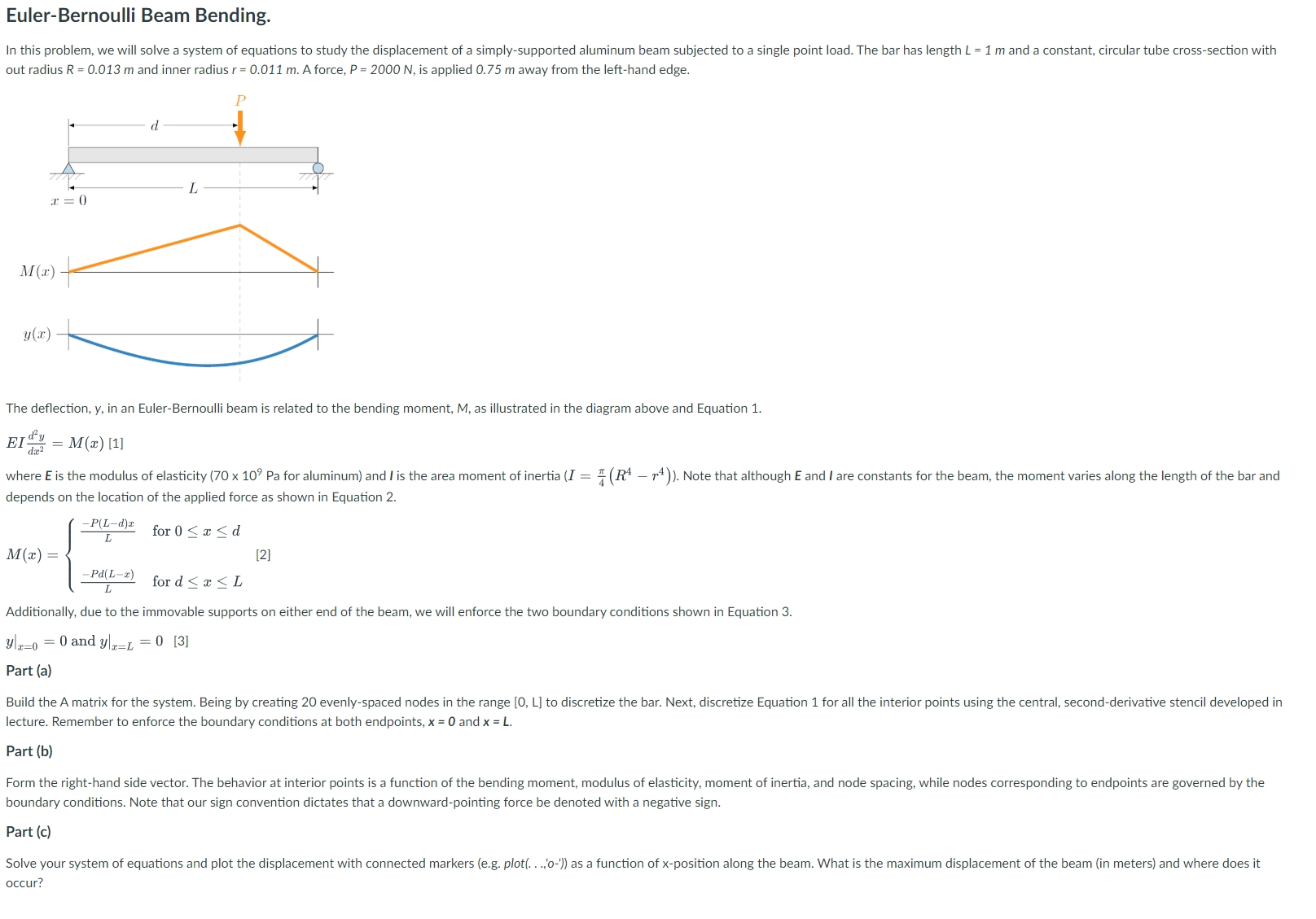
Euler$-$Bernoulli Beam Bending.

out radius R$=0\mathrm{.}013$m and inner radius r$=0\mathrm{.}011$m$.$ A force, P$=2000$N$,$ is applied $0\mathrm{.}75$ m away from the left$-$hand edge.

The deflection, y$,$ in an Euler$-$Bernoulli beam is related to the bending moment, M$,$ as illustrated in the diagram above and Equation $1.$

EI$($d$^(2)$y$)/($dx$^(2))=$M$($x$)[1]$

depends on the location of the applied force as shown in Equation $2.$

M$($x$)=\{((-$P$($L$-$d$)$x$)/($L$)$ for xd$),((-$Pd$($L$-$x$))/($L$)$ for dxL$)$:$\}$

Additionally, due to the immovable supports on either end of the beam, we will enforce the two boundary conditions shown in Equation $3.$

y$|\_($x$)=0=0$ and y$|\_($x$)=$L$=0$

Part $($a$)$

lecture. Remember to enforce the boundary conditions at both endpoints, x$=0$ and x$=$L$.$

Part $($b$)$

boundary conditions. Note that our sign convention dictates that a downward$-$pointing force be denoted with a negative sign.

Part $($c$)$

occur?