Question: Let f(x, y) = x2 + y, and F = {(x,y) E R x + y > 1}. Show that f(x, y) is not

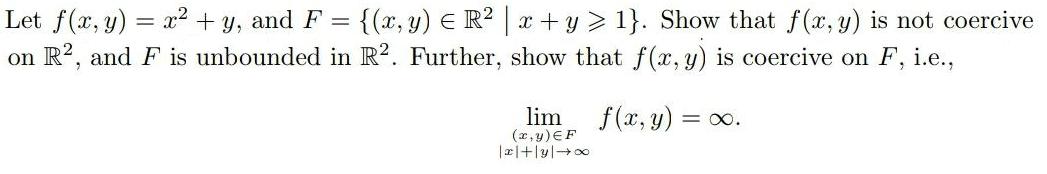
Let f(x, y) = x2 + y, and F = {(x,y) E

Let f(x, y) = x2 + y, and F = {(x,y) E R x + y > 1}. Show that f(x, y) is not coercive on R?, and F is unbounded in R?. Further, show that f(x, y) is coercive on F, i.e., %3D lim (x, y)EF f(x, y) = 0.

Step by Step Solution

★★★★★

3.28 Rating (148 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

in Heig we get Let a0 and Hoy y we have to show that tHung is not coer... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Complete the sentences with the correct responses The PE ratio is the profits-earnings ratio based on the information given: and can be to select a stock. Select which of these companies would be the...

Please give me proper solution. Calculate capacitance of parallel plate capacitor.

Quantum numbers arise naturally from the mathematics used to describe the possible states of an electron in an atom. The four quantum numbers, the principal quantum number (n), the angular momentum...

Let f(x) = 3x + 2 / x2 + 1 and g(x) = 1/ 100 cos (100x). (a) Use functional composition to form h(x) = (f g) (x), as well as j(x) = (g f) (x). (b) Find the appropriate window or windows that give a...

Let (X, Y ) be uniformly distributed in a circle of radius r about the origin. That is, their joint density is given by Let R = X2 + Y2 and = arc tanY/X denote their polar coordinates. Show that R...

15. Let X1, X2, . . . , Xn represent a random sample from a Rayleigh distribution with pdf f(x; ) x e x2/(2) x 0 a. It can be shown that E(X2 ) 2. Use this fact to construct an unbiased estimator...

1. Let f(x, y, z) = x2 +y' and E = {(x, y, z) : 0 1. Let f (x, y, z) = :r2+y2 and E { (x, y, z): O .T,2 -+y2 S 4, y 2 0, O z f 3 Convert the integral J E f (x, y, z) dV into cylindrical coordinates...

Hello, I am unsure how to solve this problem. Please help! Let f(x) = vx, g(x) = x2 - 2, and h(x) = . 1 X Find (fog o h) (x).

4. Let F = (-y, 0, x2 + y?), and S = {(x, y, s) : 4x2 + 2 4. Let F = ( y, 0, + y2), and S = {@, y, s) : 4T2 + Y2 g, z = sin (4T2 + y2)}. Compute (V x F) dS.

please do fast!! i will rate you good for sure!! Let X1, X2, Yl, and Y2 be random variables. (a) (7) Show that Cov(X1 + X2, Y1 + Y2) = Cov( X1, Y1) + Cov( X1, Y2) + Cov(X2, Y1) + Cov( X2, Y2). (b)...

The wall of a large room is covered with acoustic tile in which small holes are drilled 5.0 mm from center to center. How far can a person be from such a tile and still distinguish the individual...

Transform the model in Problem 20 into standard form and indicate the value of the slack variables at each corner point solution.

Most employment practices that illegally discriminate do so because of their disparate impact, so employers must ensure their job and educational requirements are necessary for their business. Group...

Consider a gas-fired boiler in which five coiled thin-walled, copper tubes of 25-mm diameter and 8-m length are submerged in pressurized water at 4.37 bars. The walls of the tubes are polished and...

A silicon chip of thickness L = 2.5 mm and thermal conductivity ks = 135 W/m K is cooled by boiling a saturated fluorocarbon liquid (T sat = 57C) on its surface. The electronic circuits on the...

A passive technique for cooling heat-dissipating integrated circuits involves submerging the ICs in a low boiling point dielectric fluid. Vapor generated in cooling the circuits is condensed on...

A condenser-boiler section contains a 2-m x 2-m copper plate operating at a uniform temperature of T s = 100C and separating saturated steam, which is condensing, from a saturated liquid-X, which...

The sheet metal form shown moves in the xy plane. Knowing that (vA)x = 100mm/s, (vB)y = ??75mm/s, and (vC)x = 400mm/s, determine (a) The angular velocity of the plate, (b) The velocity of point A....

What is the importance of adding A tail to a sequence during library prep in illumina sequencing

Let f (x) = (1 + x2 + x4 + . . . + x8) and g(x) = (1 + x/1! + x2/2! + . . . + x8/8! ) . (a) Define h(x) = f (x) g(x), h(x) is a polynomial of degree 8. Find the coeffi- cients of x0, x1, x2 and x3....

A car starts from a point at 2:00 pm. and travels north at 40 mph. Another car starts from the same point at 3:00 pm. and travels west at 50 mph. After the second car has traveled i h, at what rate...

Answer all questions correctly. 1) A retired Woman has $180,000 to invest. She has Chosen one relatively safe investment Fund that has an annual yield of gif. and another riskier Find that has a 13....

Let X be a nonempty set and let f : X R have bounded range in R. If a R, show that Example 2.4.l(a) implies that Sup{a + f(x) : x X} = a + sup{f(x) : x X}: Show that we also have Inf{a + f(x) : x...

Section 14.7: Problem 9 (1 point) Let f (x, y) = x2 + kxy + y2 where k is a constant. For what values of k does the Second Derivative Test guarantee that f (x, y) will have a saddle point at the...

11. [-/1 Points] DETAILS Math 110 Course Resources - Precalculus Review Course Packet on the domain of a function - Functions Course Packet on functions, domain, and range Determine the domain of...