Question: please help!!!! 1. Consider a symmetric matrix A with the following eigenvalues and two of the three corre- sponding (non-normalized) eigenvectors. A1 = 10 =-5
please help!!!!
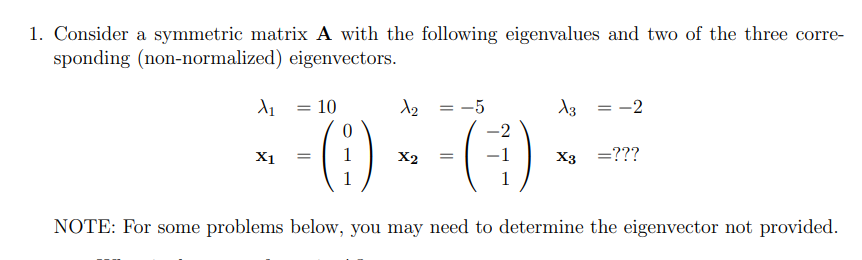


Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


