Question: Please help! 1. When working with the Mean Value Theorem, we need to be able to find secant lines quickly. Given f(a:) below, find the
Please help!
1.
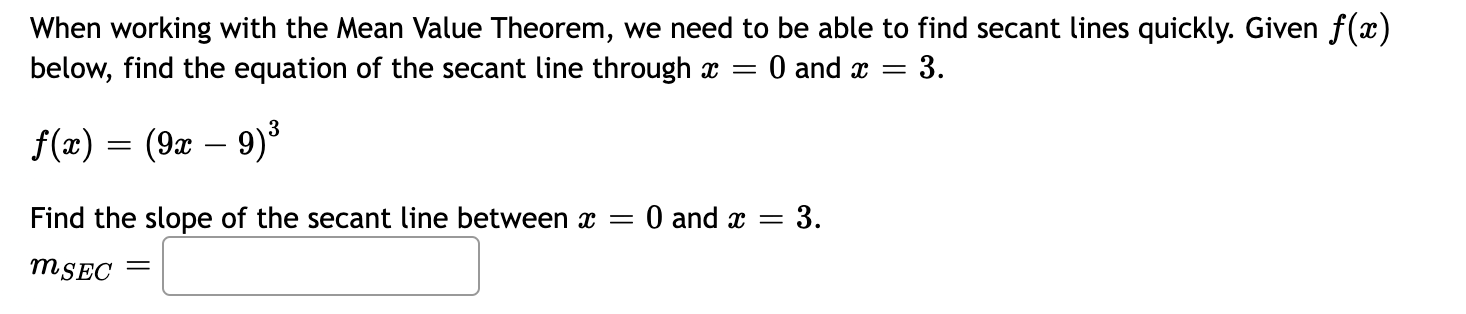




![= 4 8222 on the interval [ 1, 4]. The average rate](https://s3.amazonaws.com/si.experts.images/answers/2024/07/668902f1b99ed_217668902f1930f7.jpg)



When working with the Mean Value Theorem, we need to be able to find secant lines quickly. Given f(a:) below, find the equation of the secant line through a: = 0 and m = 3. f(:r) = (9m 9)3 Find the slope of the secant line between a; = 0 and a: = 3. Consider the function an) = 4 8222 on the interval [ 1, 4]. The average rate of change of ns) on this interval is: \"4)_\"_\" - 4 ( 1) The Mean Value Theorem says that there is at least one number c in the open interval ( 1, 4) so that f '(c) equals this average rate of change. Find the value(s) of c that work on ( 1, 4): Consider the function m) = 3m3 21: on the interval [ 5, 5]. The average rate of change of f(w) on this interval is: \"5)'\"'5)- 5(5) _ The Mean Value Theorem says that there is at least one number c in the open interval ( 5, 5) so that f '(c) equals this average rate of change. Find the value(s) of c that work on ( 5, 5): Consider the function x) = IO + 5 on the interval [3, 6]. The average rate of change of an) on this interval is: L) _ \"3) 6 (3) _ The Mean Value Theorem says that there is at least one number 0 in the open interval (3, 6) so that f '(c) equals this average rate of change. Find the value(s) of c that work on (3, 6): 1 Consider the function ns) 2 E on the interval [5, 12]. The average rate of change of f(:I:) on this interval is: L) _ K5) 12 (5) The Mean Value Theorem says that there is at least one number 0 in the open interval (5, 12) so that f '(c) equals this average rate of change. Find the value(s) of c that work on (5, 12): Consider the function x) = 29:3 12:2:2 301: + 3 on the interval [ 4, 10]. The average rate of change of f(m) on this interval is: f'1)'\"'4)- 10(4) _ The Mean Value Theorem says that there is at least one number c in the open interval ( 4, 10) so that f '(c) equals this average rate of change. Find the value(s) of c that work on ( 4, 10): Consider the function m) = 49:2 + 856 2. f(a:) is increasing on the interval ( 00, A] and decreasing on the interval [A, 00) where A is the critical number. At :3 = A, does f(a:) have a local min, a local max, or neither? Type in your answer as LMIN, LMAX, or The function at) = 23:3 279:2 + 108% + 7 has one local minimum and one local maximum. This function has a local minimum at :1: equals :] and a local maximum at 9: equals :] 4 2 Given 0 = is? 3:133 16:1:2 + 961: amnww = :J Find the critical number(s) of C(33) Use interval notation to identify where C(x) is
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


