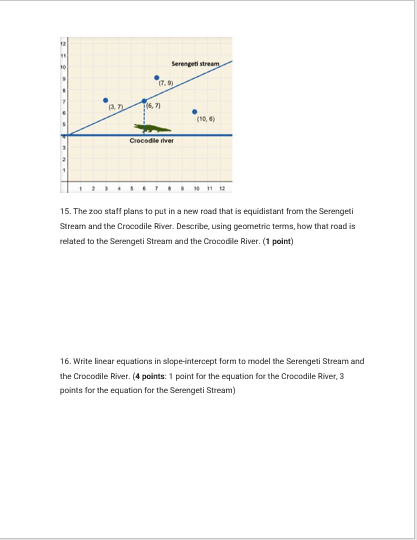
Question: Please help... 2.5.3 Practice: Modeling: Wildlife Sanctuary Practice Geometry Honors Sem 2 Name Date YOUR ASSIGNMENT: Wildlife Sanctuary You are designing a path for traveling
Please help...








Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


